Глава 14. Дополнительные соотношения между элементами в треугольнике
14.3. Доказательство некоторых формул
Доказательство:
 1
|
| Рисунок 14.3.1
|
Из основной формулы 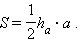
С другой стороны 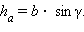
По теореме синусов 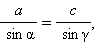 откуда
откуда 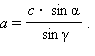
Подставляя выражения для 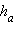 и a в основную формулу, получим искомое выражение.
и a в основную формулу, получим искомое выражение.
Доказательство: По теореме косинусов получим
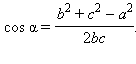 Отсюда
Отсюда
где 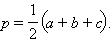 Подставляя полученное выражение в формулу
Подставляя полученное выражение в формулу 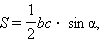 получим искомую формулу.
получим искомую формулу.
 2
|
| Рисунок 14.3.2
|
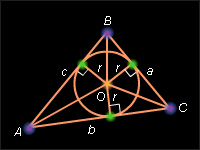
Доказательство: 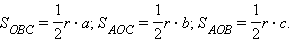
По свойству 2 площади простой фигуры имеем
Отсюда имеем искомое выражение.
Доказательство: По формуле 1 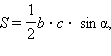 по теореме синусов
по теореме синусов 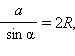 т. е.
т. е. 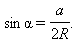 Подставляя выражение для
Подставляя выражение для 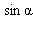 в формулу для площади треугольника, получим искомую формулу.
в формулу для площади треугольника, получим искомую формулу.
 3
|
| Рисунок 14.3.3
|
Доказательство: из теоремы синусов следует, что 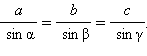 Для доказательства последнего равенства рассмотрим треугольник ABC, описанную около него окружность
Для доказательства последнего равенства рассмотрим треугольник ABC, описанную около него окружность 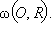 Проведем диаметр BD.
Проведем диаметр BD. 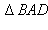 – прямоугольный, т. к.
– прямоугольный, т. к. 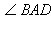 опирается на диаметр. Кроме того,
опирается на диаметр. Кроме того, 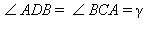 как опирающиеся на одну и ту же дугу AB. Из треугольника BAD имеем
как опирающиеся на одну и ту же дугу AB. Из треугольника BAD имеем 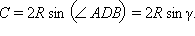 Отсюда получаем искомое равенство
Отсюда получаем искомое равенство 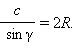
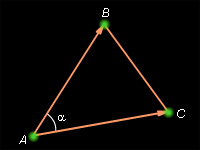 4
|
| Рисунок 14.3.4
|
Доказательство: По формуле 1 этого раздела 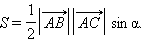 Из теоремы 11.10
Из теоремы 11.10 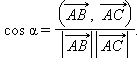 Тогда
Тогда 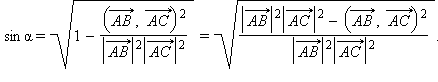 Подставляя выражение для
Подставляя выражение для 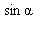 в формулу площади, получаем
в формулу площади, получаем 
Соотношения в прямоугольном треугольнике
Доказательство следует из формулы для площади треугольника.
Доказательство следует из формулы 1.
 5
|
| Рисунок 14.3.5
|
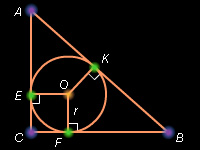
Доказательство: Пусть OE = OF = OK = r; Отсюда CE = CF = r. По свойству отрезков касательных AK = AE = b – CE = b – r. BK = BF = a – CF = a – r. Но AK + BK = AB = c. Имеем c = b – r + a – r = a + b – 2r.
Откуда получаем 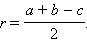
Доказательство является следствием формулы 5, если иметь в виду, что 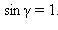
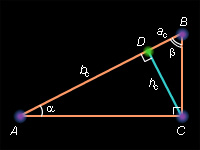 6
|
| Рисунок 14.3.6
|
Доказательство следует из подобия треугольников ADC и CDB по двум углам 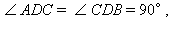
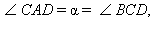 так как
так как 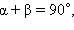 а
а 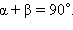 Отсюда
Отсюда 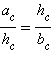 или
или 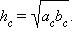
Доказательство следует из подобия треугольников ACB и CDB.
Доказательство следует из подобия треугольников ACB и ADC.
Доказательство: Первые два равенства следуют из определения синуса и косинуса острого угла прямоугольного треугольника, а последние два равенства – из определения тангенса того же угла.
Соотношения в правильном треугольнике
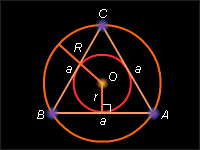 7
|
| Рисунок 14.3.7
|
Доказательство следует из формулы 1, если учесть, что 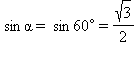 и a = b = c.
и a = b = c.
Доказательство следует из формулы 3, если учесть, что 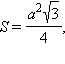
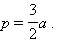
Доказательство: Следует из формулы 4, если учесть, что 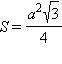
Соотношения в четырехугольниках
 8
|
| Рисунок 14.3.8
|
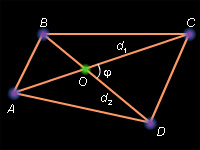
Доказательство: Пусть O – точка пересечения диагоналей четырехугольника ABCD. По свойству площадей имеем 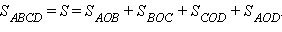 Но
Но 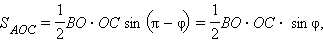
Складывая левые и правые части, имеем
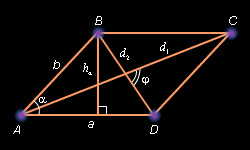
Параллелограмм
 9
|
| Рисунок 14.3.9
|
Доказательство: Первое равенство – следствие теоремы 13.3.
Второе равенство – следствие теоремы 13.3 и того, что 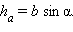
Третье равенство – следствие формулы 6.
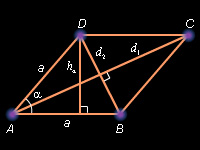
Ромб
 10
|
| Рисунок 14.3.10
|
Доказательство: Первое и второе равенства – следствие формулы 5 и того, что ромб – частный случай параллелограмма. Третье равенство – следствие формулы 6 и свойства ромба, задаваемого теоремой 7.8.
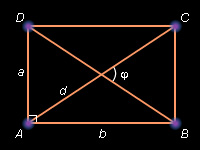
Прямоугольник
 11
|
| Рисунок 14.3.11
|
Доказательство: Следствие определения прямоугольника 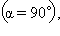 формулы 6 и свойства прямоугольника, задаваемого теоремой 7.7.
формулы 6 и свойства прямоугольника, задаваемого теоремой 7.7.
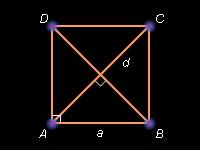
Квадрат
 12
|
| Рисунок 14.3.12
|
Доказательство: Следствие определения квадрата и формулы 6.
Трапеция
Доказательство: Первое равенство – следствие теоремы 7.12.
Второе равенство – следствие теоремы 13.5.
Правильный многоугольник
 13
|
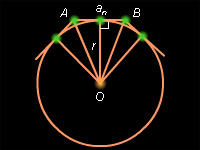
| Рисунок 14.3.13. Правильный n-угольник. r – радиус вписанной окружности.
|
Доказательство: Пусть 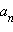 – сторона правильного n-угольника, r – радиус вписанной в него окружности. Тогда по свойству площади
– сторона правильного n-угольника, r – радиус вписанной в него окружности. Тогда по свойству площади 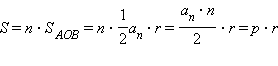 , где p – полупериметр n-угольника.
, где p – полупериметр n-угольника.
Доказательство: Первое равенство – следствие теоремы 9.4. Второе равенство – следствие формулы 3.
Окружность. Круг
Первое равенство – следствие теоремы 9.6.
Второе равенство – следствие теоремы 13.6.
Доказательство: Первое равенство – следствие определения радианной меры центрального угла. Второе равенство получается, если учесть следствие 9.4.
Доказательство: Первое равенство – следствие теоремы 13.1.
Второе равенство получается из первого, если учесть следствие 9.4.
Произвольный треугольник
 14
|
| Рисунок 14.3.14
|
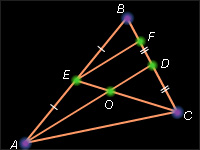
| 29. Три медианы треугольника пересекаются в одной точке. Точка пересечения делит медианы в отношении 2:1, считая от вершины. |
Это является, в частности, прямым следствием теоремы Чевы и обосновано в §14.1. Для доказательства второй части утверждения рассмотрим треугольник ABC. Пусть AD и CE – медианы этого треугольника и O – точка их пересечения. Через точку E проведем прямую, параллельную прямой AD. Пусть F – точка пересечения этой прямой со стороной BC. Очевидно, EF – средняя линия в треугольнике ABD и, следовательно, 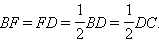 Тогда из теоремы 4.13 следует, что
Тогда из теоремы 4.13 следует, что 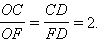 Так как медиана была выбрана произвольно, то это очевидно для любой медианы, что и завершает доказательство.
Так как медиана была выбрана произвольно, то это очевидно для любой медианы, что и завершает доказательство.
 15
|
| Рисунок 14.3.15
|
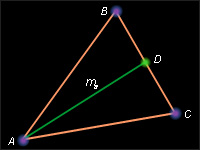
Рассмотрим произвольный треугольник ABC со сторонами AB = c, BC = a, и AC = b. Пусть 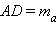 – медиана этого треугольника. Обозначим дополнительно
– медиана этого треугольника. Обозначим дополнительно 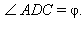 Тогда
Тогда 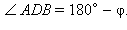
Применим теорему косинусов к треугольникам ADC и ADB. С учетом введенных обозначений имеем
Сложим правые и левые части этих равенств с учетом того, что 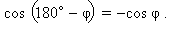 Тогда получим
Тогда получим 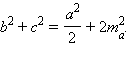 Отсюда
Отсюда 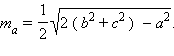
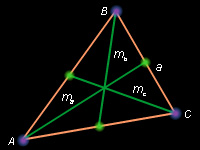 16
|
| Рисунок 14.3.16
|
Повторяя рассуждения предыдущего пункта, легко получить выражения для длин других медиан треугольника. Выпишем выражения, связывающие длины сторон треугольника и длины медиан этого же треугольника:
Рассматривая эти равенства как систему уравнений относительно a2, b2 и c2 при известных ma2, mb2 и mc2, мы можем решить ее относительно, например, 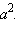 Обозначим
Обозначим 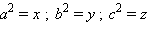 и запишем систему в виде
и запишем систему в виде
Складывая последовательно первое уравнение со вторым и третьим, получим:
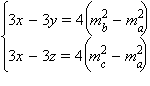 или
или 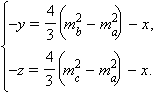
Подставим найденные выражения для y и z в первое уравнение. После приведения подобных получим
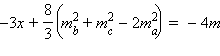 или
или 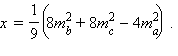
Окончательно:
 17
|
| Рисунок 14.3.17
|
| 32.
Отрезки, на которые разбивает биссектриса угла треугольника противолежащую сторону, пропорциональны сторонам этого угла
|
Пусть отрезок CD – биссектриса треугольника ABC. Обозначим 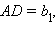
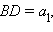
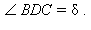 Тогда
Тогда 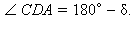 По теореме синусов в треугольнике BDC имеем
По теореме синусов в треугольнике BDC имеем
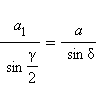 или
или 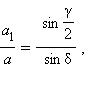 а в треугольнике ADC:
а в треугольнике ADC:
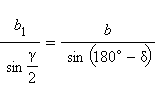 или
или 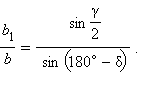
Но 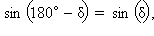 отсюда правые части равенств совпадают, следовательно, совпадают и левые:
отсюда правые части равенств совпадают, следовательно, совпадают и левые:
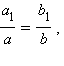 что и требовалось доказать.
что и требовалось доказать.
Применим теорему косинусов в треугольниках BDC и ADC:
Умножим, соответственно, первое равенство на b, а второе на a и вычтем после этого из первого равенства второе. Получим
Преобразуем левую часть этого равенства. Используя результат пункта 32, можно записать цепочку равенств
С другой стороны, правая часть равенства может быть преобразована к виду
Поэтому имеем
Если a = b, то треугольник ABC – равнобедренный (AC = BC), и биссектриса CD совпадает с высотой, тогда искомое выражение для 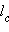 есть следствие теоремы Пифагора.
есть следствие теоремы Пифагора.
Если a ≠ b, то, сокращая эту разность, получим 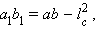 что дает искомое выражение для
что дает искомое выражение для 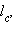 а именно:
а именно:
Площадь 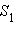 треугольника BDC равна
треугольника BDC равна 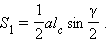 Аналогично площадь
Аналогично площадь 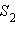 треугольника ADC равна
треугольника ADC равна 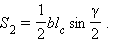 По свойству площадей
По свойству площадей 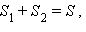 где S – площадь треугольника ABC и
где S – площадь треугольника ABC и 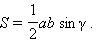 Имеем равенство
Имеем равенство
С учетом того, что 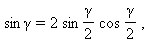 получим
получим
Из треугольника ABC, используя теорему косинусов, найдем выражение для 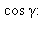
но 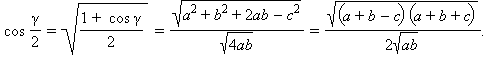
Подставляя полученное выражение в формулу для длины биссектрисы, получим искомое выражение:
 18
|
| Рисунок 14.3.18
|
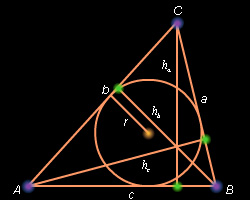
По формуле для площади S треугольника имеем
Отсюда можно найти
или, складывая почленно правые и левые части равенств, получить
С другой стороны, имеем 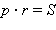 или
или 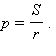 Приравнивая выражения для p и сокращая на S, получим искомое равенство:
Приравнивая выражения для p и сокращая на S, получим искомое равенство:
 19
|
| Рисунок 14.3.19
|
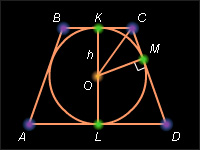
| 36.
Высота трапеции равна диаметру вписанной в нее окружности ω(O; R) |
В силу свойства 6.5 центр вписанной в трапецию окружности лежит на пересечении биссектрисы ее углов. Так как 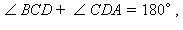 то
то 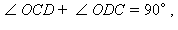 следовательно, треугольник COD – прямоугольный. В силу свойства прямоугольного треугольника, задаваемого формулой 11, квадрат длины высоты OM, опущенной на гипотенузу CD, равен произведению длин отрезков гипотенузы CM и MD, то есть
следовательно, треугольник COD – прямоугольный. В силу свойства прямоугольного треугольника, задаваемого формулой 11, квадрат длины высоты OM, опущенной на гипотенузу CD, равен произведению длин отрезков гипотенузы CM и MD, то есть
Так как CD – касательная к окружности 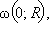 OM
OM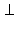 CD, то в силу единственности перпендикуляра к прямой, опущенного из данной точки вне ее, следует, что OM = R. Кроме того, из условия равнобокости трапеции и отрезков касательных CK и CM (MD и LD), проведенных из точки C(D), имеем
CD, то в силу единственности перпендикуляра к прямой, опущенного из данной точки вне ее, следует, что OM = R. Кроме того, из условия равнобокости трапеции и отрезков касательных CK и CM (MD и LD), проведенных из точки C(D), имеем
Подставляя в исходное равенство, получаем
Отсюда окончательно 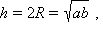 что и требовалось доказать.
что и требовалось доказать.


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


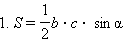

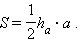
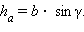
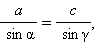 откуда
откуда 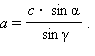
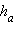 и
и 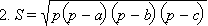
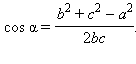 Отсюда
Отсюда 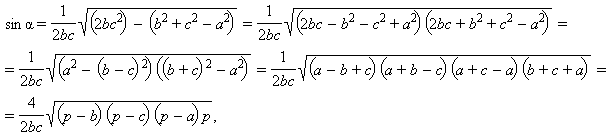
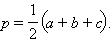 Подставляя полученное выражение в формулу
Подставляя полученное выражение в формулу 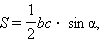 получим искомую формулу.
получим искомую формулу.
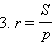

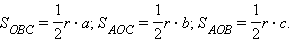
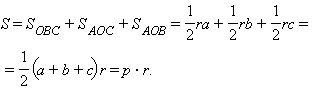
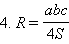
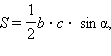 по теореме синусов
по теореме синусов 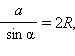 т. е.
т. е. 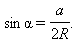 Подставляя выражение для
Подставляя выражение для 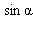 в формулу для площади треугольника, получим искомую формулу.
в формулу для площади треугольника, получим искомую формулу.
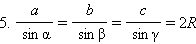

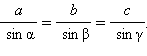 Для доказательства последнего равенства рассмотрим треугольник
Для доказательства последнего равенства рассмотрим треугольник 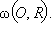 Проведем диаметр
Проведем диаметр 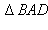 – прямоугольный, т. к.
– прямоугольный, т. к. 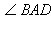 опирается на диаметр. Кроме того,
опирается на диаметр. Кроме того, 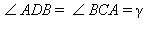 как опирающиеся на одну и ту же дугу
как опирающиеся на одну и ту же дугу 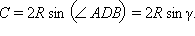 Отсюда получаем искомое равенство
Отсюда получаем искомое равенство 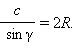
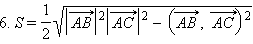

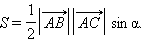 Из теоремы 11.10
Из теоремы 11.10 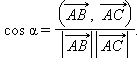 Тогда
Тогда 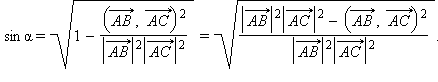 Подставляя выражение для
Подставляя выражение для 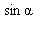 в формулу площади, получаем
в формулу площади, получаем 
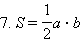
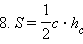
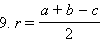

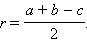
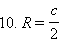
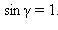
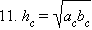

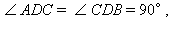
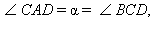 так как
так как 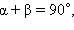 а
а 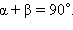 Отсюда
Отсюда 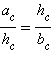 или
или 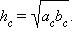
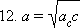
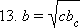
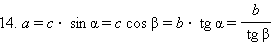
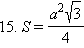

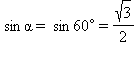 и
и 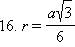
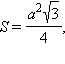
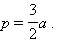
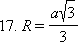
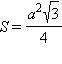
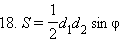

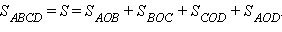 Но
Но 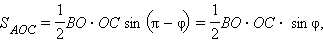
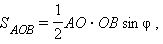
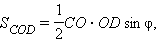
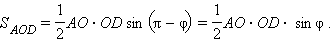
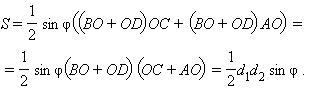
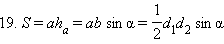

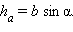
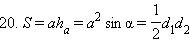

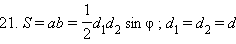

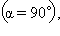 формулы 6 и свойства прямоугольника, задаваемого теоремой 7.7.
формулы 6 и свойства прямоугольника, задаваемого теоремой 7.7.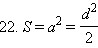

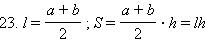
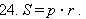

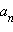 – сторона правильного
– сторона правильного 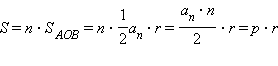 , где
, где 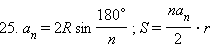
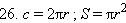
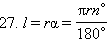
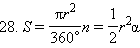

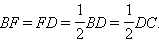 Тогда из теоремы 4.13 следует, что
Тогда из теоремы 4.13 следует, что 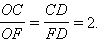 Так как медиана была выбрана произвольно, то это очевидно для любой медианы, что и завершает доказательство.
Так как медиана была выбрана произвольно, то это очевидно для любой медианы, что и завершает доказательство.

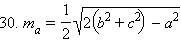
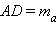 – медиана этого треугольника. Обозначим дополнительно
– медиана этого треугольника. Обозначим дополнительно 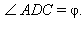 Тогда
Тогда 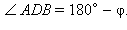
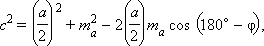
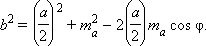
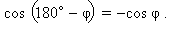 Тогда получим
Тогда получим 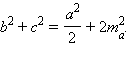 Отсюда
Отсюда 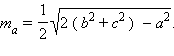
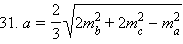

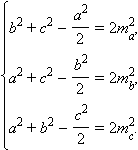
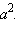 Обозначим
Обозначим 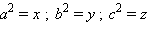 и запишем систему в виде
и запишем систему в виде
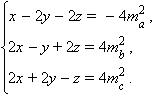
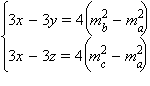 или
или 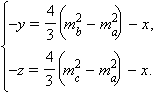
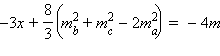 или
или 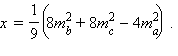
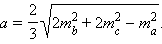

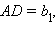
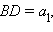
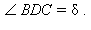 Тогда
Тогда 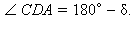 По теореме синусов в треугольнике
По теореме синусов в треугольнике 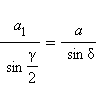 или
или 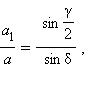 а в треугольнике
а в треугольнике 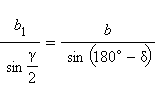 или
или 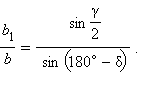
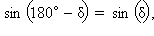 отсюда правые части равенств совпадают, следовательно, совпадают и левые:
отсюда правые части равенств совпадают, следовательно, совпадают и левые:
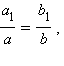 что и требовалось доказать.
что и требовалось доказать.
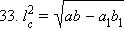
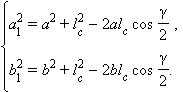
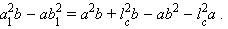
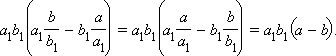
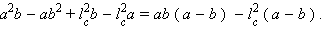
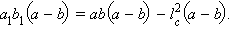
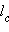 есть следствие теоремы Пифагора.
есть следствие теоремы Пифагора.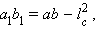 что дает искомое выражение для
что дает искомое выражение для 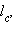 а именно:
а именно:
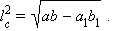
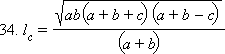
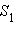 треугольника
треугольника 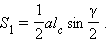 Аналогично площадь
Аналогично площадь 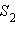 треугольника
треугольника 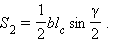 По свойству площадей
По свойству площадей 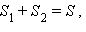 где
где 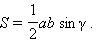 Имеем равенство
Имеем равенство
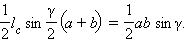
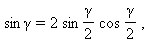 получим
получим
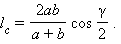
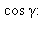
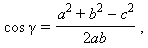
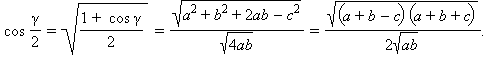
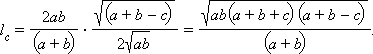
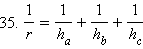

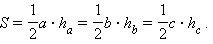
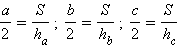
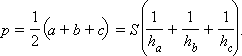
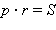 или
или 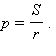 Приравнивая выражения для
Приравнивая выражения для 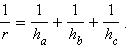

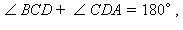 то
то 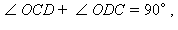 следовательно, треугольник
следовательно, треугольник 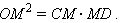
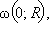
![]() CD
CD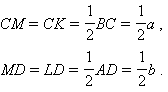
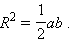
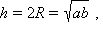 что и требовалось доказать.
что и требовалось доказать.




