 |
 |

 |
|
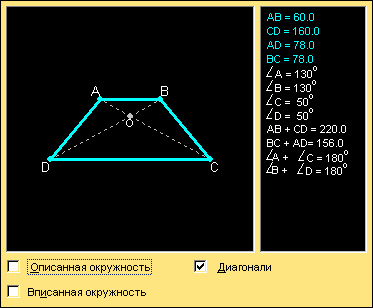
Модель 7.1.
Четырехугольник
|
Четырехугольник называется вписанным, если все его вершины лежат на окружности.

 |
|
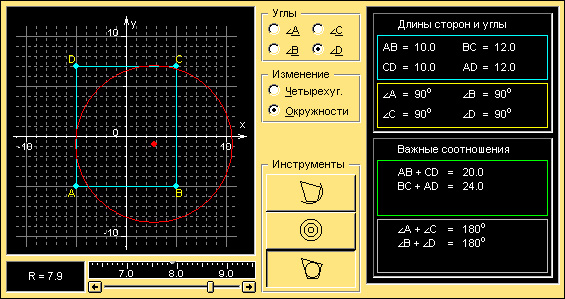
Модель 7.2.
Вписанные и описанные четырехугольники
|
Четырехугольник называется описанным, если все его стороны касаются некоторой окружности.

Для того, чтобы четырехугольник был вписанным, необходимо и достаточно, чтобы сумма его противолежащих углов равнялась

Для того, чтобы выпуклый четырехугольник был описанным, необходимо и достаточно, чтобы суммы длин его противолежащих сторон были равны.
Описанный параллелограмм является ромбом.
 |
 |
 |

