Глава 6. Окружность
6.3. Окружности, описанные около треугольника и вписанные в него
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром или медиатриссой.
Свойство 6.4.
Серединный перпендикуляр является ГМТ, равноудаленных от концов отрезка.
Теорема 6.4.
Серединные перпендикуляры к двум сторонам треугольника пересекаются.
Пусть ABC – треугольник, а a и b – серединные перпендикуляры к его сторонам AC и BC. Допустим, прямые a и b не пересекаются, то есть – параллельны. Прямая AC 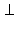 a, BC a, BC 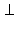 b и, следовательно, (BC) b и, следовательно, (BC) 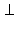 a, так как a || b. Таким образом, (AC) a, так как a || b. Таким образом, (AC) 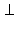 a и (BC) a и (BC) 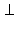 a, и, значит, (AC) || (BC). Но это неверно. Прямые AC и BC пересекаются в точке C. Полученное противоречие доказывает теорему. a, и, значит, (AC) || (BC). Но это неверно. Прямые AC и BC пересекаются в точке C. Полученное противоречие доказывает теорему.
 1
|
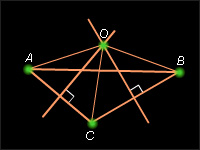
| Рисунок 6.3.1. Серединные перпендикуляры
|
|
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема 6.5.
Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.
Пусть a и b – серединные перпендикуляры к сторонам AC и BC треугольника ABC, а точка O – точка их пересечения. Из свойств серединного перпендикуляра AO = OC = OB. Следовательно, точка O лежит на серединном перпендикуляре к стороне AB. Таким образом, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Кроме того, точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Отсюда, по определению, центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам треугольника. Теорема доказана.
|
Окружность называется вписанной в треугольник, если она касается всех его сторон.
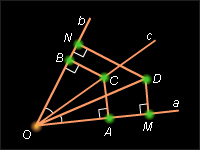
Для определения центра вписанной в треугольник окружности пользуются свойством биссектрисы угла.
Свойство 6.5.
Биссектриса угла является ГМТ, равноудаленных от его сторон.
Пусть луч c с началом в точке O является биссектрисой угла, образованного лучами a и b. Пусть C – произвольная точка биссектрисы. Опустим перпендикуляры к сторонам a и b угла из точки C, и пусть A и B соответственно основания этих перпендикуляров. Треугольники OBC и OAC равны. Действительно 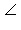 BOC = BOC = 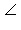 AOC, так как [OC) – биссектриса, углы при вершинах A и B прямые по построению, сторона OC общая. Следовательно, CB = CA. AOC, так как [OC) – биссектриса, углы при вершинах A и B прямые по построению, сторона OC общая. Следовательно, CB = CA.
 2
|
| Рисунок 6.3.2. Биссектриса угла
|
Теперь пусть точка D одинаково удалена от сторон угла O, т. е. DM = DN. Прямоугольные треугольники ODM и ODN равны, так как у них общая гипотенуза OD и равные катеты DM и DN. Значит, Δ DOM = Δ DON, и точка D лежит на биссектрисе угла O.
|
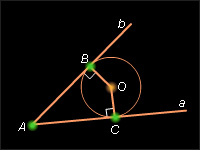
Теорема 6.6.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Пусть окружность ω (O; P) вписана в угол (ab) с вершиной A. Пусть B и C – точки касания окружности прямыми b и a соответственно. Соединим точки B и C с центром O окружности. По свойству 6.1 (OB)  b и (OC) b и (OC)  a и OB = OC = R. Таким образом, точка O равноудалена от сторон угла на расстояние, равное радиусу окружности и по свойству 6.5 принадлежит биссектрисе и только ей. Пусть теперь AMN – данный треугольник, а O – центр вписанной в него окружности. По определению окружность одновременно вписана в каждый угол треугольника и по следствию 6.4 его центр лежит на биссектрисах его углов. Следовательно, точка O лежит на пересечении всех трех биссектрис углов треугольника. Теорема доказана. a и OB = OC = R. Таким образом, точка O равноудалена от сторон угла на расстояние, равное радиусу окружности и по свойству 6.5 принадлежит биссектрисе и только ей. Пусть теперь AMN – данный треугольник, а O – центр вписанной в него окружности. По определению окружность одновременно вписана в каждый угол треугольника и по следствию 6.4 его центр лежит на биссектрисах его углов. Следовательно, точка O лежит на пересечении всех трех биссектрис углов треугольника. Теорема доказана.
 3
|
| Рисунок 6.3.3. К теореме 6.6
|
|
Теорема 6.7.
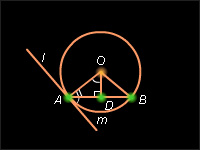
Градусная мера угла, образованного хордой и касательной к окружности, проведенной через конец хорды, равна половине градусной меры дуги, лежащей в данном плоском угле.
Пусть AB – некоторая хорда окружности ω (O; R), через конец A которой проведена касательная l к окружности .
Соединим точки A и B с центром O окружности и проведем в треугольнике AOB высоту OD на сторону AB. Треугольник AOB – равнобедренный, так как стороны AO и OB равны радиусу окружности. Поэтому высота, проведенная к основанию, является одновременно и медианой и биссектрисой. В частности, 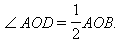 Кроме того,
Кроме того,  AOD + AOD +  OAD = 90°. С другой стороны, (OA) OAD = 90°. С другой стороны, (OA)  l по свойству касательной и, следовательно, l по свойству касательной и, следовательно, 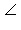 (l , (AD)) – (l , (AD)) – 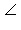 OAD = 90°. Сравнивая эти равенства, получаем OAD = 90°. Сравнивая эти равенства, получаем 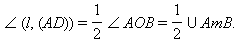 Теорема доказана.
Теорема доказана.
 4
|
| Рисунок 6.3.4. К теореме 6.7
|
|
Следствие 6.3.
Если один из лучей с вершиной в точке P касается окружности в точке C, а другой пересекает окружность в точках A и B, то AP · BP = PC2. Более коротко: квадрат отрезка касательной к окружности равен произведению отрезка секущей, проведенной из той же точки, на внешнюю ее часть.
Рассмотрим треугольники CAP и BCP. Угол CBP равен углу ACP. Действительно угол CBP – вписанный в окружность и его величина равна половине угловой величины угла CA. С другой стороны угол ACP образован хордой AC и касательной к окружности, проведенной через конец C хорды AC. По теореме 6.7 градусная мера угла ACP так же равна половине градусной меры дуги CA. Так как сумма углов любого треугольника – 180°, то углы BCP и CAP данных треугольников так же равны. Следовательно, по следствию 5.1 имеем
Из последнего равенства получаем 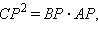
что и доказывает утверждение.
 5
|
| Рисунок 6.3.5
|
|
Теорема 6.8.
Градусная мера угла между хордами равна полусумме градусных мер дуг, принадлежащих данному плоскому углу, и соответствующему вертикальному углу.
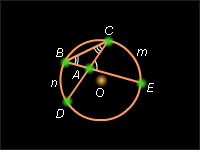
Пусть точка A лежит в круге, [AC) и [AE) – стороны угла, а точки D и B – точки пересечения с окружностью лучей, дополнительных к [AC) и [AE) соответственно. Угол CAE является внешним углом треугольника ABC и, следовательно, его величина равна сумме величин несмежных с ним углов треугольника, т.е.
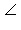 CAE = CAE = 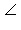 BCA + BCA +  ABC. Но углы BCA и ABC – вписанные в окружность и равны половине величины дуги CmE и BnD, соответственно. Поэтому ABC. Но углы BCA и ABC – вписанные в окружность и равны половине величины дуги CmE и BnD, соответственно. Поэтому 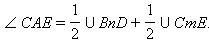 Теорема доказана.
Теорема доказана.
 6
|
| Рисунок 6.3.6. К теореме 6.8
|
|
Теорема 6.9.
Градусная мера угла между секущими равна полуразности дуг, лежащих в данном плоском угле.


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".












