Глава 6. Окружность
6.2. Окружность, угол
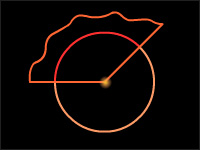
Центральным углом в окружности называется плоский угол с вершиной в ее центре. Дугой окружности, соответствующей центральному углу, называется часть окружности, расположенная внутри центрального угла.
 1
|
| Рисунок 6.2.1. Центральный угол и дуга окружности
|
 2
|
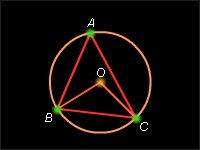
| Рисунок 6.2.2. Вписанный в окружность угол
|
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла. Угол называется вписанным в окружность, если вершина его лежит на окружности, а стороны пересекают окружность. Говорят, что вписанный угол опирается на ту дугу окружности, которая не содержит вершину вписанного угла. Так же говорят, что вписанный угол опирается на хорду, соединяющую точки пересечения окружности со сторонами угла.
Теорема 6.1.
Угол, вписанный в окружность, равен половине градусной меры дуги, на которую он опирается.
Рассмотрим сначала частный случай, когда одна из сторон угла проходит через центр окружности. Треугольник AOB – равнобедренный, так как у него стороны OA и OB равны радиусу. Поэтому углы A и B треугольника равны. А так как их сумма равна внешнему углу треугольника при вершине O, то угол B треугольника равен половине угла AOC, что и требовалось доказать.
 3
|
| Рисунок 6.2.3. К теореме 6.1
|
Общий случай сводится к рассмотренному частному случаю проведением вспомогательного диаметра BD. В случае, представленном посередине на рис. 6.2.3: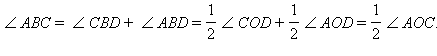 
В случае, представленном справа на том же рисунке: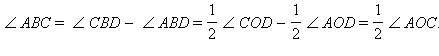 
|
Следствие 6.1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Следствие 6.2.
Углы, опирающиеся на диаметр, равны 90°.
Теорема 6.2.
Если хорды AB и CD окружности пересекаются в точке S , то AS · BS = CS · DS.
Углы ASD и BCS равны как вертикальные. Углы BAD и BCD равны по следствию 6.1. Так как сумма углов треугольника – 180°, то треугольники ASD и CSD имеют равные углы. Тогда из следствия 5.1 теоремы 5.4 имеем, в частности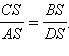 
Откуда AS · BS = CS · DS. Что и требовалось доказать.
 4
|
| Рисунок 6.2.4
|
|
Теорема 6.3.
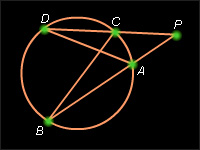
Пусть из точки P вне окружности проведены два луча, пересекающие окружность в точках A, B и C, D соответственно. Тогда AP · PB = PC · PD.
Рассмотрим треугольники PDA и PBC. Угол при вершине P – общий, угол PDA равен углу PBC по следствию 6.1, следовательно, углы треугольников PDA и PBC равны. Из следствия 5.1 теоремы 5.4 имеем, в частности,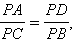 
отсюда PA · PB = PC · PD, что и требовалось доказать.
 5
|
| Рисунок 6.2.5. К доказательству теоремы 6.3
|
|
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".
