 |
 |
Две прямые, параллельные третьей, параллельны.
Это свойство называется транзитивностью параллельности прямых.
Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
Свойство параллельных прямых задается следующей теоремой, обратной к теореме 3.1.
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
На основании этой теоремы легко обосновываются следующие свойства.
Если две параллельные прямые пересечены третьей прямой, то соответствующие углы равны.
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна
Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Понятие параллельности позволяет ввести следующее новое понятие, которое в дальнейшем понадобится в 11-й главе.
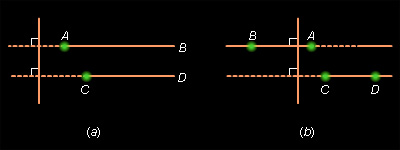
Два луча называются одинаково направленными, если существует такая прямая, что, во-первых, они перпендикулярны этой прямой, во-вторых, лучи лежат в одной полуплоскости относительно этой прямой.
Два луча называются противоположно направленными, если каждый из них одинаково направлен с лучом, дополнительным к другому.
Одинаково направленные лучи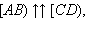 
а противоположно направленные лучи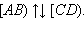 
|
| Рисунок 3.3.2 |
|
|
 |
