Глава 11. Векторы
11.1. Основные понятия и свойства
Вектором называется направленный отрезок. Если у отрезка AB его концы равноправны, то для вектора один из концов отрезка, например, A называется началом, а другой, то есть B, – концом. Обозначим вектор либо указанием концов отрезка, причем начало вектора ставится на первое место, либо строчной латинской буквой со стрелкой или чертой над буквами.
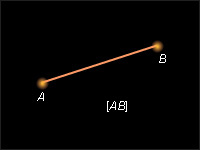 1
|
| Рисунок 11.1.1. Отрезок AB |
|
 2
|
Рисунок 11.1.2.Вектор 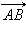 |
|
 3
|
Рисунок 11.1.3.Вектор 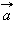 |
|
На рис. 11.1.1 изображен обычный отрезок AB, а на рис. 11.1.2 – вектор 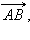 на рис. 11.1.3 – вектор
на рис. 11.1.3 – вектор 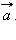
Векторы 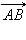 и
и 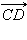 называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы
называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы 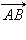 и
и 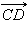 называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
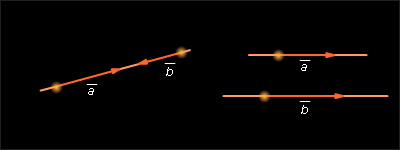 4
|
| Рисунок 11.1.4. Коллинеарные векторы
|
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора 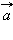 обозначим
обозначим 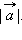 Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине. На рис. 11.1.5 вектор
Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине. На рис. 11.1.5 вектор 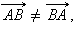 а вектор
а вектор 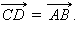
 5
|
| Рисунок 11.1.5. Равенство векторов
|
Углом между ненулевыми векторами 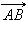 и
и 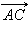 называется угол BAC. Углом между любыми двумя ненулевыми векторами
называется угол BAC. Углом между любыми двумя ненулевыми векторами 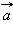 и
и 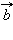 называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами равен нулю.
называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами равен нулю.
Нулевым вектором 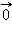 называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. Вектор называется единичным, если его абсолютная величина равна единице.
называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. Вектор называется единичным, если его абсолютная величина равна единице.
Замечание 11.1
Любую пару векторов, один из которых равен нулевому вектору будем считать коллинеарными.
Теорема 11.1.
Два вектора, сонаправленные с третьим вектором, сонаправлены.
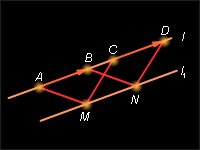
Пусть данные векторы 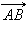 и
и 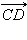 сонаправлены с вектором
сонаправлены с вектором 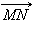 Докажем, что
Докажем, что 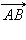 сонаправлен с
сонаправлен с 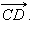
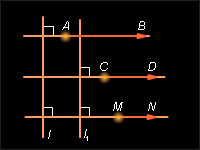 6
|
| Рисунок 11.1.6. К теореме 11.1
|
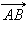 сонаправлен с сонаправлен с 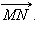 Следовательно, прямые AB и MN – параллельны, и существует такая прямая l, перпендикулярная им обеим, что лучи AB и MN лежат в одной полуплоскости от l. Следовательно, прямые AB и MN – параллельны, и существует такая прямая l, перпендикулярная им обеим, что лучи AB и MN лежат в одной полуплоскости от l.
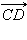 сонаправлен с сонаправлен с 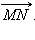 Следовательно, прямые CD и MN параллельны, и существует прямая Следовательно, прямые CD и MN параллельны, и существует прямая 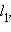 такая что лучи CD и MN лежат в одной полуплоскости.
такая что лучи CD и MN лежат в одной полуплоскости.
Так как (AB) || (MN) и (CD) || (MN), то (AB) || (CD). 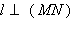 и
и 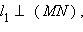 тогда по следствию 4.1
тогда по следствию 4.1 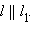 Тогда из двух полуплоскостей, которые образуются при разбиении плоскости прямыми l1 и l и содержат луч MN, одна содержит другую. Пусть эта полуплоскость ограничена прямой l и содержит луч MN. Тогда она содержит лучи MN, AB и CD. Отсюда следует, что [AB) и [CD) лежат в одной полуплоскости от прямой l и лежат на параллельных прямых и, следовательно, одинаково направлены. Отсюда векторы
Тогда из двух полуплоскостей, которые образуются при разбиении плоскости прямыми l1 и l и содержат луч MN, одна содержит другую. Пусть эта полуплоскость ограничена прямой l и содержит луч MN. Тогда она содержит лучи MN, AB и CD. Отсюда следует, что [AB) и [CD) лежат в одной полуплоскости от прямой l и лежат на параллельных прямых и, следовательно, одинаково направлены. Отсюда векторы 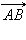 и
и 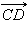 сонаправлены. Теорема доказана.
сонаправлены. Теорема доказана.
|
Свойства равенства векторов:
-
каждый вектор равен самому себе;
-
если вектор 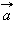 равен вектору
равен вектору 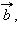 то
то 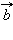 равен
равен 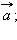
-
два вектора, равные третьему, равны.
Теорема 11.3.
Если 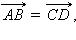 то
то 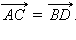
Пусть даны равные векторы 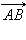 и
и 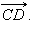 Если они не лежат на одной прямой, то согласно теореме 11.2 ABCD – параллелограмм и
Если они не лежат на одной прямой, то согласно теореме 11.2 ABCD – параллелограмм и 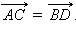
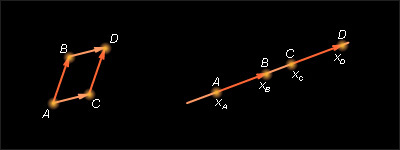
Пусть 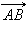 и
и 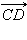 лежат на одной прямой. Введем на этой прямой координату x, и пусть числа лежат на одной прямой. Введем на этой прямой координату x, и пусть числа 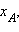 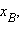 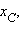 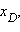 – координаты соответственно точек A, B, C, D. Тогда условие – координаты соответственно точек A, B, C, D. Тогда условие 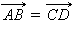 означает, что для этих координат выполнено равенство
означает, что для этих координат выполнено равенство 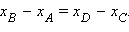 Отсюда следует, что
Отсюда следует, что 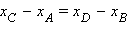 , а это означает, что
, а это означает, что 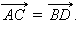
 8
|
| Рисунок 11.1.8. К теореме 11.3
|
Замечание. Равенство |xB – xA| = |xD – xC| означает равенство длин отрезков AB и CD, т. е. AB = CD; совпадение знаков разностей 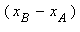 и
и 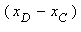 означает сонаправленность векторов
означает сонаправленность векторов 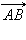 и
и 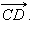
|
Пусть на плоскости Oxy точка 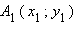 – начало вектора
– начало вектора 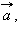 а точка
а точка 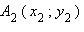 – его конец.
– его конец.
Координатами вектора 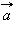 называются числа
называются числа 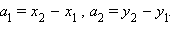 Для обозначения того, что вектор
Для обозначения того, что вектор 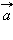 имеет координаты
имеет координаты 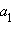 и
и 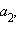 используют запись
используют запись 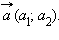 Длина отрезка
Длина отрезка 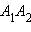 равна
равна 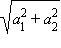 и равна по определению абсолютной величине вектора
и равна по определению абсолютной величине вектора 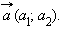 Радиус-вектором
Радиус-вектором 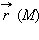 точки M (x; y) плоскости Oxy называется вектор с началом в точке O (0, 0) и концом в точке M (x; y).
точки M (x; y) плоскости Oxy называется вектор с началом в точке O (0, 0) и концом в точке M (x; y).
Теорема 11.4.
Если два вектора равны, то равны и их соответствующие координаты.
Пусть 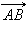 и
и 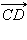 – равные векторы, где
– равные векторы, где 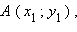 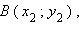 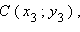 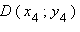 – концы отрезков AB и CD. Если – концы отрезков AB и CD. Если 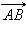 и
и 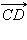 не лежат на одной прямой, то из равенства векторов следует, что четырехугольник ABCD – параллелограмм (см. теорему 11.2). Тогда x2 – x1 = x4 – x3, y2 – y1 = y4 – y3, и теорема доказана. не лежат на одной прямой, то из равенства векторов следует, что четырехугольник ABCD – параллелограмм (см. теорему 11.2). Тогда x2 – x1 = x4 – x3, y2 – y1 = y4 – y3, и теорема доказана.
 9
|
| Рисунок 11.1.9. К теореме 11.4
|
Если векторы 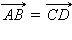 лежат на одной прямой l, рассмотрим прямую
лежат на одной прямой l, рассмотрим прямую 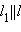 и вектор
и вектор 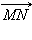 на ней, равный данным. Пусть
на ней, равный данным. Пусть 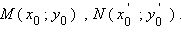 Так как
Так как 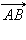 и
и 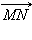 равны и лежат на параллельных прямых, из предыдущего пункта
равны и лежат на параллельных прямых, из предыдущего пункта 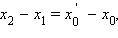 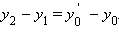 С другой стороны
С другой стороны 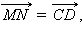 и аналогично
и аналогично 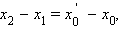 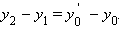 Сравнивая равенства, получаем требуемое x2 – x1 = x4 – x3, y2 – y1 = y4 – y3. Сравнивая равенства, получаем требуемое x2 – x1 = x4 – x3, y2 – y1 = y4 – y3.
|
Теорема 11.5.
Если у двух векторов соответствующие координаты равны, то эти векторы равны.
Пусть 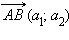 и
и 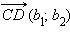 – два различных вектора, причем – два различных вектора, причем 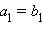 и
и 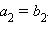 Пусть
Пусть 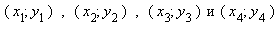 координаты соответственно точек A, B, C и D. Тогда
координаты соответственно точек A, B, C и D. Тогда 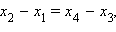
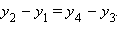 Из этих равенств следует, что
Из этих равенств следует, что 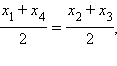 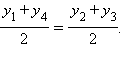
-
Если 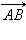 и
и 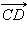 не лежат на одной прямой, то последние равенства означают, что диагонали параллелограмма ABCD при пересечении делятся пополам. Тогда ABDC – параллелограмм, и отсюда по теореме 11.2
не лежат на одной прямой, то последние равенства означают, что диагонали параллелограмма ABCD при пересечении делятся пополам. Тогда ABDC – параллелограмм, и отсюда по теореме 11.2 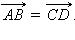
-
Если 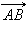 и
и 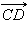 лежат на одной прямой l, рассмотрим прямую лежат на одной прямой l, рассмотрим прямую 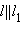 и вектор
и вектор 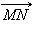 на ней, равный
на ней, равный 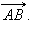 Пусть
Пусть 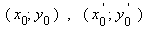 – координаты соответственно точек M и N. Тогда по теореме 11.4
– координаты соответственно точек M и N. Тогда по теореме 11.4 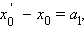 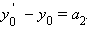 Так как векторы
Так как векторы 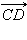 и
и 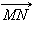 не лежат на одной прямой, и их координаты равны, то по доказанному в предыдущем пункте
не лежат на одной прямой, и их координаты равны, то по доказанному в предыдущем пункте 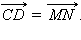 С учетом того, что
С учетом того, что 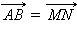 по выбору, по свойству 3 равенства векторов два вектора
по выбору, по свойству 3 равенства векторов два вектора 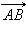 и
и 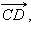 равные третьему вектору равные третьему вектору 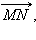 равны, т. е.
равны, т. е. 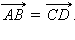 Теорема доказана.
Теорема доказана.
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


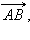 на рис. 11.1.3 – вектор
на рис. 11.1.3 – вектор 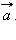
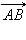 и
и 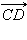 называются одинаково направленными или сонаправленными, если лучи
называются одинаково направленными или сонаправленными, если лучи 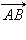 и
и 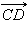 называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

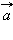 обозначим
обозначим 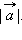 Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине. На рис. 11.1.5 вектор
Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине. На рис. 11.1.5 вектор 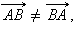 а вектор
а вектор 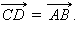

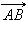 и
и 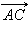 называется угол
называется угол 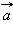 и
и 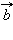 называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами равен нулю.
называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами равен нулю.
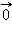 называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. Вектор называется единичным, если его абсолютная величина равна единице.
называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. Вектор называется единичным, если его абсолютная величина равна единице.

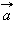 равен вектору
равен вектору 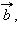 то
то 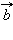 равен
равен 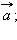

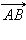 и
и 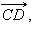 не лежащие на одной прямой. Соединим начала
не лежащие на одной прямой. Соединим начала 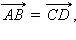 и наоборот, если
и наоборот, если 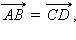 то четырехугольник
то четырехугольник 
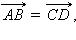 то
то 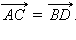
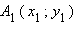 – начало вектора
– начало вектора 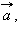 а точка
а точка 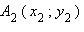 – его конец.
– его конец.
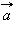 называются числа
называются числа 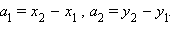 Для обозначения того, что вектор
Для обозначения того, что вектор 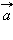 имеет координаты
имеет координаты 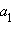 и
и 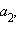 используют запись
используют запись 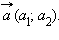 Длина отрезка
Длина отрезка  равна
равна 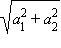 и равна по определению абсолютной величине вектора
и равна по определению абсолютной величине вектора 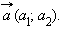 Радиус-вектором
Радиус-вектором 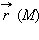 точки
точки 





