Учебник. Доказательство некоторых формул

$\mathrm{1. }S=\frac{1}{2}bċcċsin\alpha$

Доказательство:

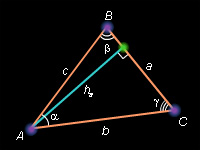
Из основной формулы $S=\frac{1}{2}{h}_aċa.$

С другой стороны $h_a=bċsin\gamma$

По теореме синусов   $\frac{a}{sin\alpha }=\frac{c}{sin\gamma }$ откуда $a=\frac{cċsin\alpha }{sin\gamma }.$

Подставляя выражения для $h_a$ и a в основную формулу, получим искомое выражение.

$\mathrm{2. }S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$

Доказательство:  По теореме косинусов получим $cos\alpha =\frac{b^2+c^2-a^2}{2bc}\mathrm{.}$ Отсюда

$\begin{array}{l}sin\alpha =\frac{1}{2bc}\sqrt{\left(2b{c}^2\right)-\left(b^2+c^2-a^2\right)}=\frac{1}{2bc}\sqrt{\left(2bc-b^2-c^2+a^2\right)\left(2bc+b^2+c^2-a^2\right)}=\\ =\frac{1}{2bc}\sqrt{\left(a^2-{\left(b-c\right)}^2\right)\left({\left(b+c\right)}^2-a^2\right)}=\frac{1}{2bc}\sqrt{\left(a-b+c\right)\left(a+b-c\right)\left(a+c-a\right)\left(b+c+a\right)}=\\ =\frac{4}{2bc}\sqrt{\left(p-b\right)\left(p-c\right)\left(p-a\right)p}\mathrm{,}\end{array}$

  где $p=\frac{1}{2}\left(a+b+c\right)$ Подставляя полученное выражение в формулу $S=\frac{1}{2}bcċsin\alpha \mathrm{,}$ получим искомую формулу.

$\mathrm{3. }r=\frac{S}{p}$

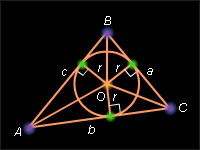
Доказательство: $S_{OBC}=\frac{1}{2}rċa\mathrm{;}{S}_{AOC}=\frac{1}{2}rċb\mathrm{;}{S}_{AOB}=\frac{1}{2}rċc\mathrm{.}$

По свойству 2 площади простой фигуры имеем

$\begin{array}{l}S=S_{OBC}+S_{AOC}+S_{AOB}=\frac{1}{2}ra+\frac{1}{2}rb+\frac{1}{2}rc=\\ =\frac{1}{2}\left(a+b+c\right)r=pċr\mathrm{.}\end{array}$

Отсюда имеем искомое выражение.

$\mathrm{4. }R=\frac{abc}{4S}$

Доказательство: По формуле 1 $S=\frac{1}{2}bċcċsin\alpha$ по теореме синусов  $\frac{a}{sin\alpha }=2R$ т. е. $sin\alpha =\frac{a}{2R}$ Подставляя выражение для $sin\alpha$ в формулу для площади треугольника, получим искомую формулу.

$\mathrm{5. }\frac{a}{sin\alpha }=\frac{b}{sin\beta }=\frac{c}{sin\gamma }=2R$

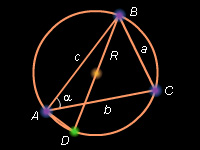
Доказательство: из теоремы синусов следует, что $\frac{a}{sin\alpha }=\frac{b}{sin\beta }=\frac{c}{sin\gamma }$ Для доказательства последнего равенства рассмотрим треугольник ABC, описанную около него окружность $\omega \left(O\mathrm{,}R\right)$ Проведем диаметр BD. $\Delta BAD$ – прямоугольный, т. к. $\angle BAD$ опирается на диаметр. Кроме того, $\angle ADB=\angle BCA=\gamma$ как опирающиеся на одну и ту же дугу AB. Из треугольника BAD имеем $C=2Rsin\left(\angle ADB\right)=2Rsin\gamma$ Отсюда получаем искомое равенство $\frac{c}{sin\gamma }=2R$

$\mathrm{6. }$

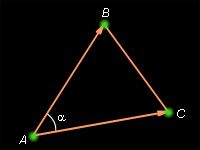
Доказательство: По формуле 1 этого раздела $S$ Из теоремы 11.10 $cos$ Тогда $sin$ Подставляя выражение для $sin$ в формулу площади, получаем $S$

Соотношения в прямоугольном треугольнике $\mathrm{7. }S=\frac{1}{2}aċb$

Доказательство следует из формулы для площади треугольника.

$\mathrm{8. }S=\frac{1}{2}cċh_c$

Доказательство следует из формулы 1.

$\mathrm{9. }r=\frac{a+b-c}{2}$

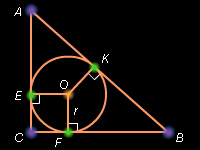
Доказательство: Пусть OE = OF = OK = r; Отсюда CE = CF = r. По свойству отрезков касательных AK = AE = b – CE = b – r.  BK = BF = a – CF = a – r. Но AK + BK = AB = c. Имеем c = b – r + a – r = a + b – 2r. Откуда получаем $r=\frac{a+b-c}{2}$

$\mathrm{10. }R=\frac{c}{2}$

Доказательство является следствием формулы 5, если иметь в виду, что $sin\gamma =1.$

$\mathrm{11. }$

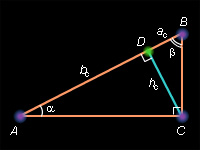
Доказательство следует из подобия треугольников ADC и CDB по двум углам $\angle ADC=\angle CDB={90}^{ˆ},$ $\angle CAD=\alpha =\angle BCD\mathrm{,}$ так как $\alpha +\beta ={90}^{ˆ}$ а $\alpha +\beta ={90}^{ˆ}$ Отсюда $\frac{a_c}{h_c}=\frac{h_c}{b_c}$ или $h_c$

$\mathrm{12. }$

Доказательство следует из подобия треугольников ACB и CDB.

$\mathrm{13. }$

Доказательство следует из подобия треугольников ACB и ADC.

$\mathrm{14. }a=cċsin\alpha =ccos\beta =bċtg\alpha =\frac{b}{tg\beta }$

Доказательство: Первые два равенства следуют из определения синуса и косинуса острого угла прямоугольного треугольника, а последние два равенства – из определения тангенса того же угла.

Соотношения в правильном треугольнике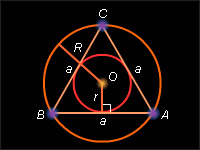 $\mathrm{15. }S=\frac{a^2\sqrt{3}}{4}$

Доказательство следует из формулы 1, если учесть, что $sin\alpha =sin{60}^{ˆ}=\frac{\sqrt{3}}{2}$ и a = b = c.

$\mathrm{16. }r=\frac{a\sqrt{3}}{6}$

Доказательство следует из формулы 3, если учесть, что $S=\frac{a^2\sqrt{3}}{4}$  $p=\frac{3}{2}a.$

$\mathrm{17. }R=\frac{a\sqrt{3}}{3}$

Доказательство: Следует из формулы 4, если учесть, что $S=\frac{a^2\sqrt{3}}{4}$

Соотношения в четырехугольниках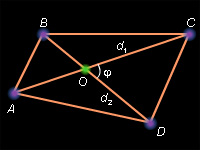 $\mathrm{18. }S=\frac{1}{2}{d}_1{d}_{2}sin\phi$

Доказательство: Пусть O – точка пересечения диагоналей четырехугольника ABCD. По свойству площадей имеем $S_{ABCD}=S=S_{AOB}+S_{BOC}+S_{COD}+S_{AOD}$ Но $S_{AOC}=\frac{1}{2}BOċOCsin\left(\pi -\phi \right)=\frac{1}{2}BOċOCċsin\phi \mathrm{,}$

$S_{AOB}=\frac{1}{2}AOċOBsin\phi ,$ $S_{COD}=\frac{1}{2}COċODsin\phi \mathrm{,}$ $S_{AOD}=\frac{1}{2}AOċODsin\left(\pi -\phi \right)=\frac{1}{2}AOċODċsin\phi .$

Складывая левые и правые части, имеем

$\begin{array}{l}S=\frac{1}{2}sin\phi \left(\left(BO+OD\right)OC+\left(BO+OD\right)AO\right)=\\ =\frac{1}{2}sin\phi \left(BO+OD\right)\left(OC+AO\right)=\frac{1}{2}{d}_1{d}_{2}sin\phi .\end{array}$ Параллелограмм $\mathrm{19. }S=a{h}_a=absin\alpha =\frac{1}{2}{d}_1{d}_{2}sin\alpha$

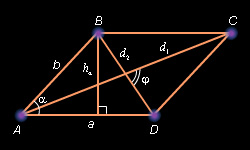
Доказательство: Первое равенство – следствие теоремы 13.3. Второе равенство – следствие теоремы 13.3 и того, что $h_a=bsin\alpha$

Третье равенство – следствие формулы 6.

Ромб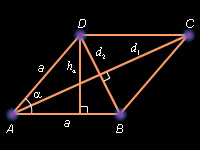 $\mathrm{20. }S=a{h}_a=a^{2}sin\alpha =\frac{1}{2}{d}_1{d}_2$

Доказательство: Первое и второе равенства – следствие формулы 5 и того, что ромб – частный случай параллелограмма. Третье равенство – следствие формулы 6 и свойства ромба, задаваемого теоремой 7.8.

Прямоугольник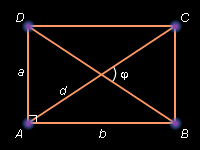 $\mathrm{21. }S=ab=\frac{1}{2}{d}_1{d}_{2}sin\phi ;d_1=d_2=d$

Доказательство: Следствие определения прямоугольника  $\left(\alpha ={90}^{ˆ}\right)$ формулы 6 и свойства прямоугольника, задаваемого теоремой 7.7.

Квадрат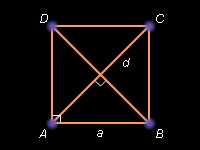 $\mathrm{22. }S=a^2=\frac{d^2}{2}$

Доказательство: Следствие определения квадрата и формулы 6.

Трапеция $\mathrm{23. }l=\frac{a+b}{2};S=\frac{a+b}{2}ċh=lh$

Доказательство: Первое равенство – следствие теоремы 7.12. Второе равенство – следствие теоремы 13.5.

Правильный многоугольник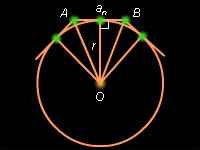 $\mathrm{24. }S=pċr.$

Правильный n-угольник. r – радиус вписанной окружности.

Доказательство: Пусть $a_n$ – сторона правильного n-угольника, r – радиус вписанной в него окружности. Тогда по свойству площади $S=nċS_{AOB}=nċ\frac{1}{2}{a}_nċr=\frac{a_nċn}{2}ċr=pċr$ , где – полупериметр -угольника.

$\mathrm{25. }{a}_n=2Rsin\frac{{180}^{ˆ}}{n};S=\frac{n{a}_n}{2}ċr$

Доказательство: Первое равенство – следствие теоремы 9.4. Второе равенство – следствие формулы 3.

Окружность. Круг $\mathrm{26. }c=2\pi r;S=\pi r^2$

Первое равенство – следствие теоремы 9.6. Второе равенство – следствие теоремы 13.6.

$\mathrm{27. }l=r\alpha =\frac{\pi r{n}^{ˆ}}{{180}^{ˆ}}$

Доказательство: Первое равенство – следствие определения радианной меры центрального угла. Второе равенство получается, если учесть следствие 9.4.

$\mathrm{28. }S=\frac{\pi r^2}{{360}^{ˆ}}n=\frac{1}{2}{r}^2\alpha$

Доказательство: Первое равенство – следствие теоремы 13.1.

Второе равенство получается из первого, если учесть следствие 9.4.

Произвольный треугольник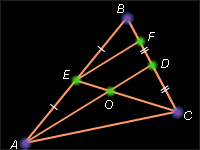

29. Три медианы треугольника пересекаются в одной точке. Точка пересечения делит медианы в отношении 2:1, считая от вершины.

Это является, в частности, прямым следствием теоремы Чевы и обосновано в §14.1. Для доказательства второй части утверждения рассмотрим треугольник ABC. Пусть AD и CE – медианы этого треугольника и O – точка их пересечения. Через точку E проведем прямую, параллельную прямой AD. Пусть F – точка пересечения этой прямой со стороной BC. Очевидно, EF – средняя линия в треугольнике ABD и, следовательно, $BF=FD=\frac{1}{2}BD=\frac{1}{2}DC\mathrm{.}$ Тогда из теоремы 4.13 следует, что $\frac{OC}{OF}=\frac{CD}{FD}=2$ Так как медиана была выбрана произвольно, то это очевидно для любой медианы, что и завершает доказательство.

$\mathrm{30. }{m}_a=\frac{1}{2}\sqrt{2\left(b^2,+,c^2\right)-a^2}$

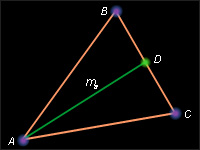
Рассмотрим произвольный треугольник ABC со сторонами AB = c, BC = a, и AC = b. Пусть $AD=m_a$ – медиана этого треугольника. Обозначим дополнительно $\angle ADC=\phi$ Тогда $\angle ADB={180}^{ˆ}-\phi$

Применим теорему косинусов к треугольникам ADC и ADB. С учетом введенных обозначений имеем

$c^2={\left(\frac{a}{2}\right)}^2+m_a^2-2\left(\frac{a}{2}\right)m_{a}cos\left({180}^{ˆ}-\phi \right)\mathrm{,}$ $b^2={\left(\frac{a}{2}\right)}^2+m_a^2-2\left(\frac{a}{2}\right)m_{a}cos\phi \mathrm{.}$

Сложим правые и левые части этих равенств с учетом того, что $cos\left({180}^{ˆ},-,\phi \right)=\mathrm{-}\cos \phi .$ Тогда получим $b^2+c^2=\frac{a^2}{2}+2m_a^2\mathrm{.}$ Отсюда $m_a=\frac{1}{2}\sqrt{2(b^2+c^2)-a^2}\mathrm{.}$

$\mathrm{31. }a=\frac{2}{3}\sqrt{2m_b^2+2m_c^2-m_a^2}$

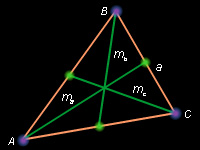
Повторяя рассуждения предыдущего пункта, легко получить выражения для длин других медиан треугольника. Выпишем выражения, связывающие длины сторон треугольника и длины медиан этого же треугольника:

$\{\begin{array}{l}{b}^2+c^2-\frac{a^2}{2}=2m_a^2\mathrm{,}\\ a^2+c^2-\frac{b^2}{2}=2m_b^2\mathrm{,}\\ a^2+b^2-\frac{c^2}{2}=2m_c^2\mathrm{.}\end{array}$

Рассматривая эти равенства как систему уравнений относительно a², b² и c² при известных m_a², m_b² и m_c², мы можем решить ее относительно, например, $a^2$ Обозначим $a^2=x;b^2=y;c^2=z$ и запишем систему в виде

$\{\begin{array}{l}x-2y-2z=-4m_a^2,\\ 2x-y+2z=4m_b^2,\\ 2x+2y-z=4m_c^2.\end{array}$

Складывая последовательно первое уравнение со вторым и третьим, получим:

$\{\begin{array}{l}3x-3y=4\left(m_b^2,-,m_a^2\right)\\ 3x-3z=4\left(m_c^2,-,m_a^2\right)\end{array}$   или $\{\begin{array}{l}\mathrm{-}y=\frac{4}{3}\left(m_b^2,-,m_a^2\right)-x\mathrm{,}\\ \mathrm{-}z=\frac{4}{3}\left(m_c^2,-,m_a^2\right)-x\mathrm{.}\end{array}$

Подставим найденные выражения для y и z в первое уравнение. После приведения подобных получим

$\mathrm{-}3x+\frac{8}{3}\left(m_b^2,+,m_c^2,-,2,m_a^2\right)=-4m$ или $x=\frac{1}{9}\left(8,m_b^2,+,8,m_c^2,-,4,m_a^2\right).$

Окончательно:

$a=\frac{2}{3}\sqrt{2m_b^2+2m_c^2-m_a^2}\mathrm{.}$

32.  Отрезки, на которые разбивает биссектриса угла треугольника противолежащую сторону, пропорциональны сторонам этого угла

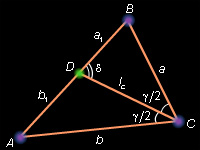
Пусть отрезок CD – биссектриса треугольника ABC. Обозначим $AD=b_1\mathrm{,}$ $BD=a_1\mathrm{,}$ $\angle BDC=\delta .$ Тогда $\angle CDA={180}^{ˆ}-\delta \mathrm{.}$ По теореме синусов в треугольнике BDC имеем

$\frac{a_1}{sin\frac{\gamma }{2}}=\frac{a}{sin\delta }$ или $\frac{a_1}{a}=\frac{sin\frac{\gamma }{2}}{sin\delta },$ а в треугольнике ADC:

$\frac{b_1}{sin\frac{\gamma }{2}}=\frac{b}{sin\left({180}^{ˆ},-,\delta \right)}$ или $\frac{b_1}{b}=\frac{sin\frac{\gamma }{2}}{sin\left({180}^{ˆ},-,\delta \right)}.$

Но $sin\left({180}^{ˆ},-,\delta \right)=sin\left(\delta \right)\mathrm{,}$ отсюда правые части равенств совпадают, следовательно, совпадают и левые: $\frac{a_1}{a}=\frac{b_1}{b},$ что и требовалось доказать.

$\mathrm{33. }{l}_c^2=\sqrt{ab-a_1{b}_1}$

Применим теорему косинусов в треугольниках BDC и ADC: $\{\begin{array}{l}{a}_1^2=a^2+l_c^2-2a{l}_{c}cos\frac{\gamma }{2},\\ b_1^2=b^2+l_c^2-2b{l}_{c}cos\frac{\gamma }{2}\mathrm{.}\end{array}$

Умножим, соответственно, первое равенство на b, а второе на a и вычтем после этого из первого равенства второе. Получим $a_1^{2}b-a{b}_1^2=a^{2}b+l_c^{2}b-a{b}^2-l_c^{2}a.$

Преобразуем левую часть этого равенства. Используя результат пункта 32, можно записать цепочку равенств

$a_1{b}_1\left(a_1,\frac{b}{b_1},-,b_1,\frac{a}{a_1}\right)=a_1{b}_1\left(a_1,\frac{a}{a_1},-,b_1,\frac{b}{b_1}\right)=a_1{b}_1\left(a,-,b\right)\mathrm{.}$

С другой стороны, правая часть равенства может быть преобразована к виду

$a^{2}b-a{b}^2+l_c^{2}b-l_c^{2}a=ab(a-b)-l_c^2(a-b)\mathrm{.}$

Поэтому имеем $a_1{b}_1\left(a,-,b\right)=ab\left(a,-,b\right)-l_c^2\left(a,-,b\right)\mathrm{.}$

Если a = b, то треугольник ABC – равнобедренный (AC = BC), и биссектриса CD совпадает с высотой, тогда искомое выражение для $l_c$ есть следствие теоремы Пифагора.

Если a ≠ b, то, сокращая эту разность, получим $a_1{b}_1=ab-l_c^2,$ что дает искомое выражение для $l_c$ а именно: $l_c^2=\sqrt{ab-a_1{b}_1}.$

$\mathrm{34. }{l}_c=\frac{\sqrt{ab\left(a,+,b,+,c\right)\left(a,+,b,-,c\right)}}{\left(a,+,b\right)}$

Площадь $S_1$ треугольника BDC равна $S_1=\frac{1}{2}a{l}_{c}sin\frac{\gamma }{2}.$ Аналогично площадь $S_2$ треугольника ADC равна $S_2=\frac{1}{2}b{l}_{c}sin\frac{\gamma }{2}.$ По свойству площадей  $S_1+S_2=S,$ где S – площадь треугольника ABC и $S=\frac{1}{2}absin\gamma .$ Имеем равенство $\frac{1}{2}{l}_{c}sin\frac{\gamma }{2}\left(a,+,b\right)=\frac{1}{2}absin\gamma \mathrm{.}$ С учетом того, что $sin\gamma =2sin\frac{\gamma }{2}cos\frac{\gamma }{2},$ получим $l_c=\frac{2ab}{a+b}cos\frac{\gamma }{2}.$

Из треугольника ABC, используя теорему косинусов, найдем выражение для $cos\gamma$

$cos\gamma =\frac{a^2+b^2-c^2}{2ab},$

но $cos\frac{\gamma }{2}=\sqrt{\frac{1+cos\gamma }{2}}=\frac{\sqrt{a^2+b^2+2ab-c^2}}{\sqrt{4ab}}=\frac{\sqrt{\left(a,+,b,-,c\right)\left(a,+,b,+,c\right)}}{2\sqrt{ab}}\mathrm{.}$

Подставляя полученное выражение в формулу для длины биссектрисы, получим искомое выражение:

$l_c=\frac{2ab}{\left(a,+,b\right)}ċ\frac{\sqrt{\left(a,+,b,-,c\right)}}{2\sqrt{ab}}=\frac{\sqrt{ab\left(a,+,b,+,c\right)\left(a,+,b,-,c\right)}}{\left(a,+,b\right)}\mathrm{.}$ $\mathrm{35. }\frac{1}{r}=\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}$

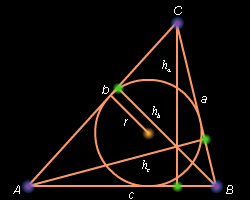
По формуле для площади S треугольника имеем

$S=\frac{1}{2}aċh_a=\frac{1}{2}bċh_b=\frac{1}{2}cċh_c.$

Отсюда можно найти

$\frac{a}{2}=\frac{S}{h_a};\frac{b}{2}=\frac{S}{h_b};\frac{c}{2}=\frac{S}{h_c}$

или, складывая почленно правые и левые части равенств, получить

$p=\frac{1}{2}\left(a,+,b,+,c\right)=S\left(\frac{1}{h_a},+,\frac{1}{h_b},+,\frac{1}{h_c}\right)\mathrm{.}$

С другой стороны, имеем $pċr=S$ или $p=\frac{S}{r}.$ Приравнивая выражения для p и сокращая на S, получим искомое равенство:

$\frac{1}{r}=\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}.$

36.  Высота трапеции равна диаметру вписанной в нее окружности ω(O; R)

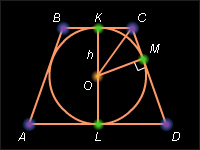
В силу свойства 6.5 центр вписанной в трапецию окружности лежит на пересечении биссектрисы ее углов. Так как $\angle$ то $\angle$ следовательно, треугольник COD – прямоугольный. В силу свойства прямоугольного треугольника, задаваемого формулой 11, квадрат длины высоты OM, опущенной на гипотенузу CD, равен произведению длин отрезков гипотенузы CM и MD, то есть

$O$

Так как CD – касательная к окружности $\omega$  OM⊥CD, то в силу единственности перпендикуляра к прямой, опущенного из данной точки вне ее, следует, что OM = R. Кроме того, из условия равнобокости трапеции и отрезков касательных CK и CM (MD и LD), проведенных из точки C(D), имеем

$\begin{array}{l}CM=CK=\frac{1}{2}BC=\frac{1}{2}a,\\ MD=LD=\frac{1}{2}AD=\frac{1}{2}b.\end{array}$

Подставляя в исходное равенство, получаем

$R^2=\frac{1}{2}ab.$

Отсюда окончательно $h=2R=\sqrt{ab},$ что и требовалось доказать.