Открытая Математика. Планиметия. Теорема Чевы

Теорема Чевы

Пусть на сторонах треугольника ABC выбраны точки $A_{1} \in B C, B_{1} \in A C, C_{1} \in A B .$ Отрезки $A A_{1}$ , $B B_{1}$ и $C C_{1}$ пересекаются в одной точке тогда и только тогда, когда выполняется равенство:

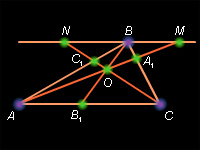
\frac{A B_{1}}{B_{1} C} ċ \frac{C A_{1}}{A_{1} B} ċ \frac{B C_{1}}{C_{1} A} = 1.

Необходимость. Пусть отрезки $A A_{1}, B B_{1}$ и $C C_{1}$ пересекаются в одной точке O. Проведем через вершину B треугольника прямую a∥AC (рис. 14.1.1). Пусть прямые $A A_{1}$ и $B B_{1}$ пересекают прямую a в точках M и N соответственно. Тогда из подобия треугольников $A A_{1} C$ и $M A_{1} B_{1}$ по двум углам ( $∠ A_{1} C A = ∠ A_{1} B M$ как накрест лежащие и $∠ B A_{1} M = ∠ A A_{1} C$ как вертикальные) имеем:

\frac{C A_{1}}{A_{1} B} = \frac{A C}{M B} .

Аналогично из подобия треугольников $A C_{1} C$ и $B C_{1} N$ по двум углам ( $∠ C_{1} C A = C_{1} N B$ и $∠ C_{1} A C = ∠ C_{1} B N$ – как пары накрест лежащих):

\frac{B C_{1}}{C_{1} A} = \frac{B N}{A C} .

Наконец, из подобия треугольников OAC и OMN по двум углам ( $∠ O C A = ∠ O N P$ и $∠ O A C = ∠ O M N$ ) получаем $\frac{A B_{1}}{B_{1} C} = \frac{M B}{B N} .$

Перемножив соответственно правые и левые части выписанных равенств, получим необходимое равенство.

Достаточность. Пусть выполнено равенство. Покажем, что отрезки $A A_{1}, B B_{1}$ и $C C_{1}$ проходят через одну точку.

Пусть O – точка пересечения отрезков $A A_{1}$ и $C C_{1},$ а C' – точка пересечения отрезка AB с лучом CO. Тогда из только что доказанного следует, что $\frac{A B_{1}}{B_{1}^{} C} ċ \frac{C A_{1}}{A_{1}^{} B} ċ \frac{B C_{}^{'}}{C^{'} A} = 1.$

Сравнивая с условием теоремы, получим $\frac{B C_{}^{'}}{C^{'} A} = \frac{B C_{1}}{C_{1}^{} A} .$ Следовательно, точки C' и $C_{1}$ совпадают.

Наряду с приведенной теоремой в приложениях бывает необходимо использовать обобщение этой теоремы. Прежде чем дать его формулировку, сделаем предварительно необходимые соглашения. На прямой AB возьмем произвольную точку C, отличную от точек A и B. Тогда векторы $\overset{⟶}{A C}$ и $\overset{⟶}{C B}$ коллинеарны. Так как $\overset{⟶}{C B} \neq \overset{⟶}{0},$ то $\overset{⟶}{A C} = λ \overset{⟶}{C B} .$ Отсюда, если точка C лежит на отрезке AB, то $\overset{⟶}{A C} ↑ ↑ \overset{⟶}{C B}$ и $λ = \frac{A C}{C B} > 0,$ если же C лежит вне отрезка AB, то $\overset{⟶}{A C} ↑ ↓ \overset{⟶}{C B}$ и $λ = - \frac{A C}{C B} < 0.$ Будем в дальнейшем понимать отношение $\frac{A C}{C B}$ отрезков AC и CB, лежащих на одной прямой «со знаком», в описанном выше смысле.

Пусть прямые a, b, c проходят через вершины A, B, C треугольника ABC и пересекают прямые BC, CA, AB в точках

A_{1}, B_{1}, C_{1}

соответственно (рис. 14.1.2). Тогда прямые a, b, c пересекаются в одной точке или параллельны тогда и только тогда, когда имеет место равенство

\frac{A B_{1}}{B_{1} C} ċ \frac{C A_{1}}{A_{1} B} ċ \frac{B C_{1}}{C_{1} A} = 1.

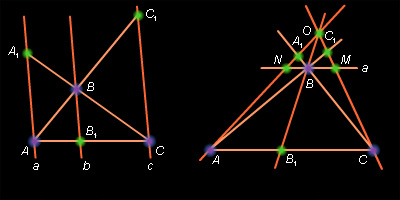
Для случая параллельных прямых (слева на рисунке 14.1.2) из теоремы Фалеса имеем соотношение $\frac{A B_{1}}{B_{1} C} = \frac{A_{1} B}{B C}, \frac{B C_{1}}{C_{} A} = \frac{B_{} C}{C A_{1}}, \frac{C A_{1}}{A_{1} B} = \frac{C A_{1}}{A_{1} B} .$

Перемножая левые и правые части равенств, получаем искомое равенство.

Обратно, пусть выполнено необходимое условие и при этом $A A_{1} ∥ C C_{1} .$ Тогда, проведя через вершину B прямую $b | | A A_{1},$ найдем точку B' ее пересечения с прямой AC. Как и в случае доказательства первой теоремы, получим $\frac{A B'}{B' C} = \frac{A B_{1}}{B_{1} C} = λ .$ Если λ > 0, то B' и B₁ делят отрезок AC в одном отношении и, следовательно, совпадают. Если λ < 0, то точки B' и B₁ лежат вне отрезка AC по одну сторону от точки A или С в зависимости от того, лежат ли точки A₁ на отрезке BC или точка C₁ на отрезке AB и снова следует из равенства с необходимостью совпадение точек B₁ и B'. Для рассмотрения общего случая снова проведем через вершину B прямую a параллельную прямой AC (справа на рисунке 14.1.2). Треугольник AC₁C подобен треугольнику BC₁M. Отсюда следует $\frac{B C_{1}}{A C_{1}} = \frac{B M_{}}{A C_{}};$ из подобия треугольников AA₁C и NA₁B получаем $\frac{A_{1} C}{A_{1} B} = \frac{A C_{}}{N B_{}} .$ Наконец, из гомотетичности относительно центра O треугольников ONM и OAC имеем $\frac{A B_{1}}{B_{1} C} = \frac{N B_{}}{B M_{}} .$ Перемножая соответственно левые и правые части равенств, получаем искомое равенство. Доказательство достаточности аналогично случаю основной теоремы.

Приведем некоторые следствия из теоремы Чевы.

Медианы треугольника пересекаются в одной точке. В этом случае

\frac{A B_{1}}{B_{1} C} = \frac{C A_{1}}{A_{1} B} = \frac{B C_{1}}{C_{1} A} = 1.

Биссектрисы треугольника пересекаются в одной точке.

Действительно из свойства биссектрис можно записать следующие равенства:

\frac{A B_{1}}{B_{1} C} = \frac{A B_{}}{B C_{}}; \frac{C A_{1}}{A_{1} B} = \frac{C A_{}}{A B_{}}; \frac{B C_{1}}{C_{1} A} = \frac{B C_{}}{C A_{}} .

Перемножая соответственно левые и правые части этих равенств, получим условие теоремы Чевы.

Прямые, соединяющие вершины треугольника с точками касания вписанного в него треугольника, пересекаются в одной точке. Эта точка называется точкой Жергона. Из свойства касательных, проведенных из одной точки к окружности имеем: AB₁ = AC₁; BA₁ = BC₁ и CA₁ = CB₁. Отсюда следует равенство из теоремы Чевы и доказательство следствия 14.3.

Высоты треугольника пересекаются в одной точке.

Рассмотрим 2 случая.

Пусть треугольник ABC остроугольный (рис. 14.1.3, a). Имеем $A C_{1} = A C cos ∠ A;$ $B C_{1} = B C cos ∠ B;$ $B A_{1} = A B cos ∠ B;$ $C A_{1} = A C cos ∠ C;$ $C B_{1} = B C cos ∠ C,$ $A B_{1} = A B cos ∠ A .$ Отсюда следует $\frac{A B cos ∠ A}{B C cos ∠ C} ċ \frac{A C cos ∠ C}{A B cos ∠ B} ċ \frac{B C cos ∠ B}{A C cos ∠ A} \equiv 1.$ Следствие доказано.
Пусть треугольник ABC тупоугольный (рис. 14.1.3, b). Применим в этом случае обобщенную теорему Чевы. Тогда аналогично случаю 1 можно записать такие же соотношения с учетом знака. Имеем $A C_{1} = A C cos ∠ A;$ $B C_{1} = B C cos ∠ B;$ $B A_{1} = A B cos ∠ B;$ $C A_{1} = A C cos ∠ C;$ $C B_{1} = B C cos ∠ C,$ $A B_{1} = A B cos ∠ A .$ Отсюда следует доказательство.

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Теорема Чевы

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ