Глава 9. Координаты и векторы в пространстве

9.9. Вычисление углов в пространстве

Понятие о скалярном произведении позволяет достаточно просто определять углы между прямыми в пространстве. Действительно, пусть в пространстве заданы две прямые с направляющими векторам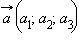и  и 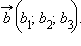Пусть угол между этими прямыми равен φ. Тогда угол между векторами может быть равен φ или 180° – φ в зависимости от того, как направлены эти вектора. Однако в любом случае модуль скалярного произведения этих векторов равен

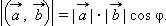Отсюда следует, что 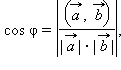так как 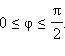Итак, угол между двумя прямыми может быть найден через координаты направляющих векторов так

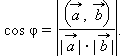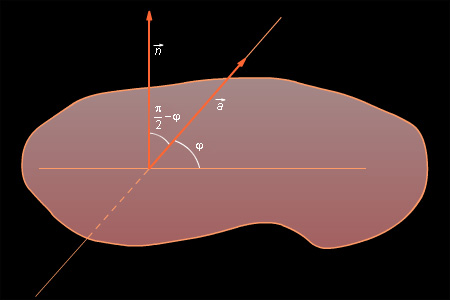
Покажем теперь, как можно вычислять угол между прямой и плоскостью. Поскольку угол между прямой и плоскостью есть угол между этой прямой и ее проекцией на эту плоскость, сведем данную задачу к предыдущей. Заметим, что угол между направляющим вектором рассматриваемой прямой и нормальным вектором равен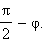

1

Рисунок 9.9.1

Этот угол уже легко вычисляется: 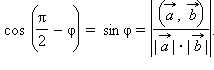Значит угол между прямой и плоскостью равен

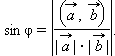Найдем, наконец, угол между двумя плоскостями, если известны их нормальные векторы. Несложно сообразить, что угол между плоскостями равен углу между их нормалями. Докажите это утверждение самостоятельно.

Значит, угол между плоскостями может быть найден по формуле:
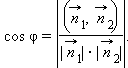