Глава 9. Координаты и векторы в пространстве

9.10. Вычисление расстояний в пространстве

Формула расстояния между точками в декартовой прямоугольной системе координат была получена в параграфе 9.4.

Для определения расстояния от точки 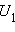W до прямой p можно, выбрав на прямой p какие-нибудь две точки, например и подсчитать стороны треугольника 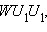а затем его высоту 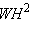WH. Сделать это нетрудно, выражая двумя способами. А именно, из прямоугольного треугольника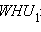 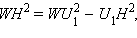  а из прямоугольного треугольника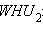 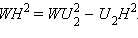  Таким образом, 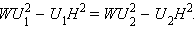Из этого равенства можно найти один из отрезков 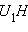и 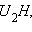затем найти 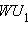WH. Не останавливаясь здесь на доказательстве, отметим, что из последнего равенства предпочтительней находить больший из этих отрезков. Ясно, что если, например, отрезок больше отрезка 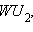то и отрезок 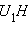больше отрезка 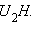Сделав в таком случае в последнем равенстве замену 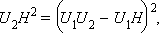найдем отрезок 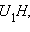а затем и высоту WH.

В некоторых случаях для вычисления расстояния 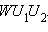WH бывает целесообразней выразить двумя способами площадь треугольника Например, так:
и

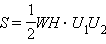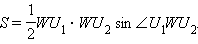Тогда из равенства
можно найти искомое расстояние WH.

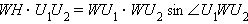Расстояние от точки до плоскости удобнее искать векторным методом. Итак, пусть задана точка 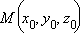и некоторая плоскость α: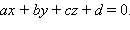

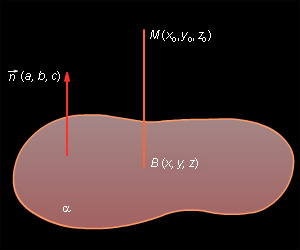
1

Рисунок 9.10.1

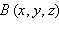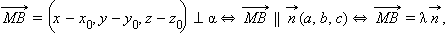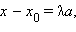
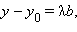
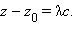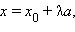
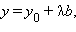
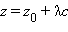Пусть точка – ортогональная проекция точки M на плоскость α. Тогда а значит,    Точка B лежит в плоскости α, ее координаты    удовлетворяют уравнению плоскости:

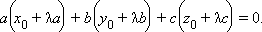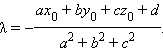Расстояние от точки 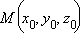до плоскости α равно 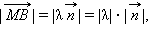значит

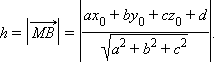Эта формула и выражает расстояние между точкой и плоскостью.