Глава 3. Перпендикулярность прямых и плоскостей
3.5. Угол между наклонной и плоскостью
Определение 3.7. Углом между наклонной и плоскостью называется угол между наклонной и ее ортогональной проекцией на плоскость.
На чертеже 3.5.1 показана наклонная AB, OB = ПрαAB, 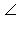 ABO – угол между наклонной AB и плоскостью α. Если прямая параллельна плоскости, то угол между ними по определению равен 0°. Если прямая перпендикулярна плоскости, то угол между ними равен 90°. Если β – угол между прямой и плоскостью, то 0° < β < 90°. Проведем в плоскости α произвольную прямую b через точку B так, чтобы OC
ABO – угол между наклонной AB и плоскостью α. Если прямая параллельна плоскости, то угол между ними по определению равен 0°. Если прямая перпендикулярна плоскости, то угол между ними равен 90°. Если β – угол между прямой и плоскостью, то 0° < β < 90°. Проведем в плоскости α произвольную прямую b через точку B так, чтобы OC  b. Пусть
b. Пусть 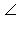 ABO = β,
ABO = β, 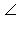 OBC = γ,
OBC = γ, 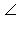 ABC = φ. Рассматривая прямоугольные треугольники ABO, OBC, ACB, имеем
ABC = φ. Рассматривая прямоугольные треугольники ABO, OBC, ACB, имеем
Заметим, что 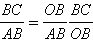 или
или
Мы получили формулу трех косинусов. Обратите внимание на то, что плоскости углов β и γ взаимно перпендикулярны.
Замечание. Поскольку углы φ, β и γ острые, из формулы трех косинусов следует, что cos β > cos φ и 0° < β < φ.
Таким образом, углом β между наклонной и ее ортогональной проекцией на плоскость является наименьший из углов, образованных наклонной с прямыми плоскости α.


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".



![]() ABO
ABO![]() b
b![]() ABO = β
ABO = β![]() OBC = γ
OBC = γ![]() ABC = φ
ABC = φ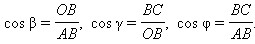
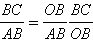 или
или




