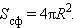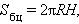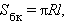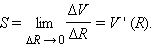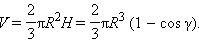Глава 7. Объемы и поверхности круглых тел
7.4. Площади поверхности цилиндра, конуса, шара
Пользуясь формулой объема шара, можно получить формулу площади поверхности шара, то есть сферы. Рассмотрим произвольный многогранник, описанный вокруг сферы, имеющей радиус R. Тогда объем многогранника можно найти по формуле 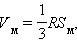 где
где 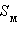 – площадь поверхности многогранника. Будем увеличивать число граней многогранника так, что площадь каждой грани неограниченно уменьшается. Получим, что объем шара выражается формулой
– площадь поверхности многогранника. Будем увеличивать число граней многогранника так, что площадь каждой грани неограниченно уменьшается. Получим, что объем шара выражается формулой 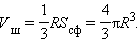 Таким образом, площадь сферы выражается формулой
Таким образом, площадь сферы выражается формулой
В главе 5 фактически уже были получены формулы для вычисления площадей поверхности цилиндра и конуса. Поэтому приведем их здесь еще раз без вывода.
Площадь поверхности цилиндра
где R – радиус основания цилиндра, H – его высота.
Площадь поверхности конуса
где R – радиус основания конуса, l – длина его образующей.
Рассмотрим площадь поверхности сферы и шарового сегмента.
Определение 7.3. Площадь поверхности шарового сегмента можно определить как предел отношения приращения объема соответствующего шарового сектора к приращению радиуса, когда приращение радиуса стремится к нулю:
 1
|
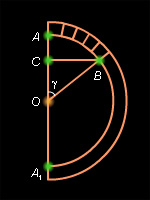
| Рисунок 7.4.1
|
На рис. 7.4.1 изображен полукруг радиуса R = OB = OA и половина плоского сегмента ACB. При вращении этого полукруга вокруг оси AA1 получается шар радиуса R, шаровой сектор с углом γ между осью и образующей, и шаровой сегмент. Высота H шарового сегмента есть:
| H = AC = OA – OC = R – R cos γ = R (1 – cos γ).
|
Объем шарового сектора
Дадим радиусу R приращение ΔR. Тогда объем шарового сегмента получит приращение ΔV, где ΔV – объем фигуры, полученной при вращении заштрихованной на рис. 7.4.1 части полукольца.
В процессе приращения объема изменяется только R, а угол γ остается постоянным, поэтому S = V' (R) = 2πR2 (1 – cos γ) = 2πRH, где S – площадь сферической части поверхности шарового сегмента (или сектора). Принимая H = 2R, получаем площадь поверхности сферы


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


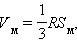 где
где 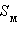 – площадь поверхности многогранника. Будем увеличивать число граней многогранника так, что площадь каждой грани неограниченно уменьшается. Получим, что объем шара выражается формулой
– площадь поверхности многогранника. Будем увеличивать число граней многогранника так, что площадь каждой грани неограниченно уменьшается. Получим, что объем шара выражается формулой 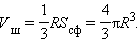 Таким образом, площадь сферы выражается формулой
Таким образом, площадь сферы выражается формулой