Пусть a и b – скрещивающиеся прямые (чертеж 3.4.1). Через прямую b проведем плоскость α, параллельную прямой a, а через прямую a – плоскость β, перпендикулярную плоскости α. Пусть α 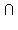 β  = c. По теореме о следе c || a. Пусть c  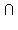b = A. В плоскости β проводим перпендикуляр AB к прямой a. Заметим, что AB – общий перпендикуляр прямых a и b. Действительно, по теореме 3.9 имеем AB  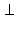α, следовательно, AB  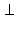b. Кроме того, AB  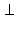a по построению. Пусть CD – отрезок с концами на данных прямых a и b ( 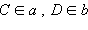), 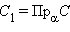. Поскольку a || α, то 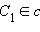и . 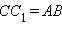Кроме того, 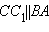, следовательно, 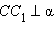. Видно, что 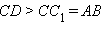, то есть AB – кратчайшее расстояние между точками прямых a и b. Это расстояние равно расстоянию между прямой a и плоскостью α. Ранее было доказано, что пара скрещивающихся прямых определяет единственную пару параллельных плоскостей. Упомянутое расстояние и есть расстояние между этими плоскостями.

Пусть a и b – данные скрещивающиеся прямые. Выберем на прямой a точку A и на прямой b точку B. Через точки A и B проведем прямые и соответственно такие, что   Образуется две пары пересекающихся прямых параллельных прямым другой пары. По признаку параллельности плоскостей эти пары прямых определяют две параллельные плоскости, в которых и лежат данные скрещивающиеся прямые.