Пусть прямая a является линией пересечения плоскостей α и β (чертеж 3.3.1). Пусть плоскость γ, перпендикулярная прямой a, пересекает плоскости α и β по прямым m и n, которые взаимно перпендикулярны, то есть γ α = m, γ β = n и mn. Такие плоскости α и β называются взаимно перпендикулярными.
Это определение не зависит от плоскости γ. Действительно, если провести другую плоскость δ, перпендикулярную прямой a, то δ || γ.
Пусть δ 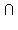α = m', δ 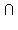β = n'. По теореме о следах m' || m и n' || n. Угол, образованный прямыми m' и n', и угол, образованный прямыми m и n, равны как углы с соответственно параллельными и одинаково направленными сторонами.
Теорема 3.8. Признак перпендикулярности двух плоскостей.
Пусть a α, a β, тогда β α. То есть, если плоскость β содержит прямую a, перпендикулярную плоскости α, то плоскости α и β перпендикулярны.
Пусть a α, a β и α β = b (чертеж 3.3.2), c – прямая, лежащая в плоскости α и проходящая через точку O пересечения прямой a с плоскостью α и с b. Через прямые a и c проведем плоскость γ. Имеем γ b, так как ab и cb. Поскольку ac, то по определению β α.
Теорема 3.9.
Пусть α β, α β = a, ba, b β, тогда b α. То есть прямая b, лежащая в одной из взаимно перпендикулярных плоскостей β и перпендикулярная линии пересечения a этих плоскостей, перпендикулярна и другой плоскости α.
Пусть ba = A (чертеж 3.3.3), a = α β и β α. В плоскости α проведем прямую c через точку A перпендикулярно прямой a. Проведем плоскость γ через прямые b и c. Имеем γ a по признаку перпендикулярности прямой и плоскости. Поскольку α β, то bc, следовательно, ba и bc, откуда следует, что b α.
Теорема 3.10.
Если плоскости α и β взаимно перпендикулярны, и к плоскости α проведен перпендикуляр, имеющий общую точку с плоскостью β, то этот перпендикуляр лежит в плоскости β.
Теорема 3.11.
Пусть плоскости α и β перпендикулярны плоскости γ и пересекаются по прямой a, тогда a 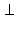γ.
На прямой a выберем произвольную точку A (чертеж 3.3.4). Проведем через точку A перпендикуляр к плоскости γ. По теореме 3.9 этот перпендикуляр лежит в каждой из плоскостей α, β, следовательно, он лежит на линии их пересечения.
α = m
n
β
