Глава 1. Арифметика

1.4.

1.4.2.

Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:

1. Коммутативность сложения:
   

   z1 + z2 = z2 + z1

   для любых   .
2. Ассоциативность сложения:
   

   (z1 + z2) + z3 = z1 + (z2 + z3)

   для любых .
3. Существует такое число z = 0, которое обладает свойством
   

   z + 0 = z

   для любого z  .
4. Для любых двух чисел z₁ и z₂ существует такое число z, что z₁ + z = z₂. Такое число z называется разностью двух комплексных чисел и обозначается z = z₂ – z₁.
5. Коммутативность умножения:
   

   z1z2 = z2z1

   для любых   .
6. Ассоциативность умножения:
   

   (z1z2)z3 = z1(z2z3)

   для любых   .
7. Дистрибутивность сложения относительно умножения:
   

   z1(z2 + z3) = z1z2 + z1z3

   для любых   .
8. Для любого комплексного числа z:
   

   z · 1 = z.

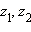
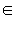
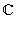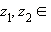
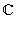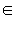
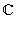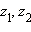
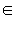
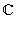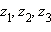
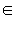
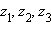
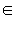
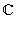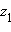9. Для любых двух чисел и 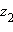существует такое число 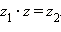z, что Такое число 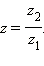z называется частным двух комплексных чисел и обозначается Деление на 0 невозможно.

Все указанные свойства доказываются с помощью определения операций сложения и умножения.

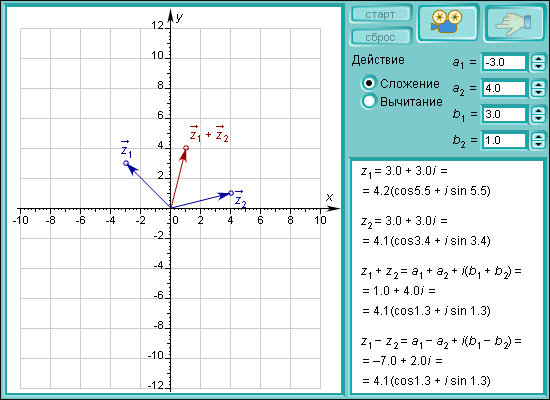
Модель 1.15. Сложение и вычитание комплексных чисел

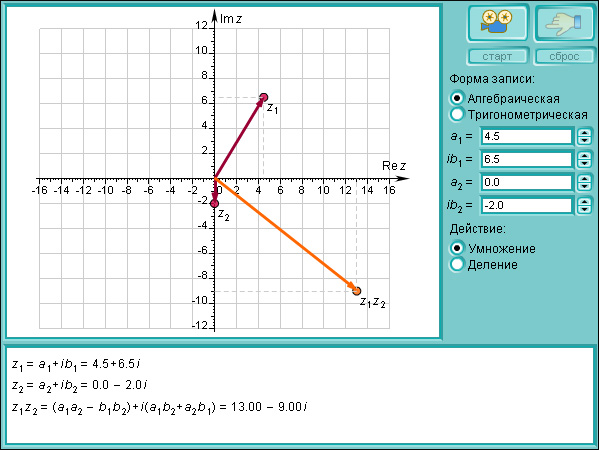
Модель 1.16. Умножение и деление комплексных чисел

	Если число z = a + bi, то число называется комплексно сопряжённым с числом z.

1

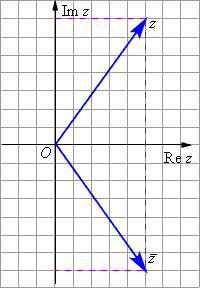Рисунок 1.4.2.1. Комплексно сопряжённые числа

Комплексно сопряжённое число обозначается 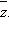Для этого числа справедливы соотношения:


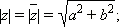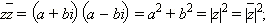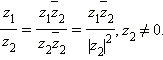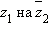Заметим, что последнее соотношение сводит операцию деления комплексных чисел к умножению и последующему делению на действительное число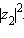