Глава 1. Арифметика
1.4.
1.4.1.
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается 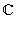 . Мы установили, что
. Мы установили, что 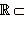
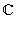 ,
а именно
,
а именно 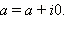
В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i. Чисто мнимое число i1 = 1i = i обладает удивительным свойством:
Таким образом,
С учётом этого замечательного соотношения легко получаются формулы сложения и умножения для комплексных чисел. Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства 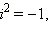 то и перемножать эти числа можно как многочлены. В самом деле,
то и перемножать эти числа можно как многочлены. В самом деле,
то есть как раз получается нужная формула.
Пример 1Вычислить z1 + z2 и z1z2, где z1 = 1 + 2i и z2 = 2 – i.
Имеем
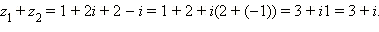
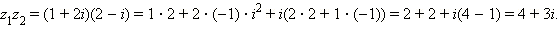
Ответ. z1 + z2 = 3 + i, z1z2 = 4 + 3i.
|
 1 1
|
| Рисунок 1.4.1.1
|
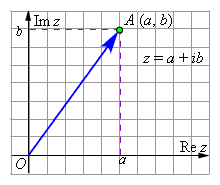
Мы хорошо помним, что геометрической интерпретацией действительных чисел является действительная прямая. Кроме того, как было установлено выше, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.
Очень важной является интерпретация комплексного числа z = a + ib как вектора 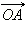 с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор
с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор 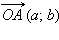 и наоборот, каждому вектору
и наоборот, каждому вектору 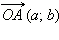 соответствует, и притом единственное, число z = a + ib.
соответствует, и притом единственное, число z = a + ib.
Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости.

 |
|
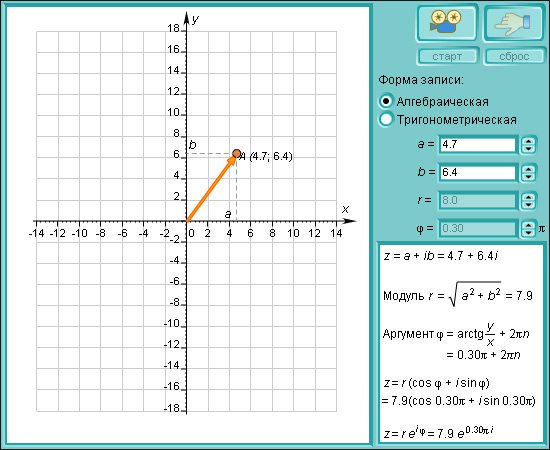
Модель 1.14.
Комплексные числа на плоскости
|
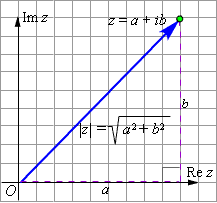
Модуль комплексного числа z обычно обозначается 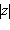 или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис.).
или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис.).
 2 2
|
| Рисунок 1.4.1.2
|
Если 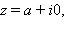 то
то 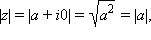 то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что
то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что 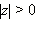 для всех
для всех 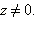 При этом
При этом
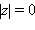 тогда и только тогда, когда
тогда и только тогда, когда 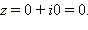
Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.
Отметим следующий важный факт: заданием своего модуля и аргумента комплексное число фиксируется однозначно. Обратное, вообще говоря, неверно: если задано комплексное число z ≠ 0, то его модуль определяется однозначно, а аргумент – нет. Действительно, если φ = arg z – аргумент этого комплексного числа, то все числа вида φ + 2πn также будут аргументами этого комплексного числа. Например, аргументами комплексного числа z = 1 + i являются углы 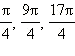 и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение –π ≤ arg z ≤ π.
и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение –π ≤ arg z ≤ π.
Заданием только лишь своего модуля определяется только комплексное число z = 0.
Из определения тригонометрических функций следует, что φ = arg z тогда и только тогда, когда для этого φ выполняется система
Пример 2Найти модуль и аргумент комплексного числа z = –1 – i.
Так как Re z = –1 и Im z = –1, то точка z лежит в третьей координатной четверти.
Для поиска аргумента решим систему
Ответ. 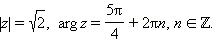
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


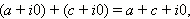
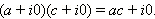
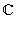 . Мы установили, что
. Мы установили, что 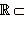
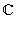 ,
а именно
,
а именно 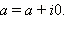
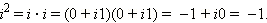
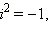 то и перемножать эти числа можно как многочлены. В самом деле,
то и перемножать эти числа можно как многочлены. В самом деле,
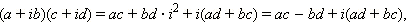

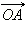 с координатами
с координатами 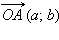 и наоборот, каждому вектору
и наоборот, каждому вектору 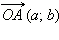 соответствует, и притом единственное, число
соответствует, и притом единственное, число 





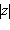 или
или 
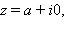 то
то 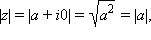 то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что
то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что 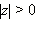 для всех
для всех 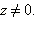 При этом
При этом
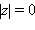 тогда и только тогда, когда
тогда и только тогда, когда 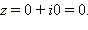




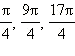 и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение
и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение