Глава 11. Векторы

11.3. Базис. Общая декартова система координат

Базисом на плоскости называются два любых неколлинеарных вектора этой плоскости, взятые в определенном порядке.

Пусть 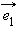  и 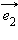 – некоторый базис и  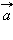– произвольный вектор, тогда по теореме 11.9 и следствию 11.1 существуют два единственным образом определенных числа x и y, такие, что

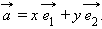Числа 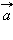x и y называются координатами вектора  в данном базисе. В этом случае также пишут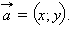

Справедливы следующие свойства.

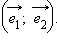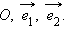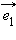Пусть на плоскости заданы точка O и произвольный базис   Совокупность этого базиса и точки O называется декартовой системой координат   Точка O называется началом координат. Если через эту точку O провести прямые в направлениях, заданных базисными векторами  и 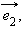 то полученные прямые называются осями координат: прямая OX – осью абсцисс, прямая Oy – осью ординат. Координаты радиус-вектора точки M называются координатами этой точки в данной системе координат (x – абцисса, y – ордината).

1

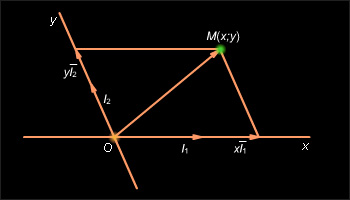
Рисунок 11.3.1

Если  и 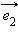 взаимно перпендикулярны и их модули равны единице, то базис называется ортонормированным, и мы получим известную нам прямоугольную декартову систему координат на плоскости. Таким образом, рассмотренная здесь декартова система координат  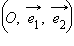является обобщением рассмотренной ранее прямоугольной декартовой системы координат, которая в свою очередь является частным случаем общей декартовой системы координат.

Мы видели (теорема 11.12), что свойства сложения и умножения вектора на число, записанные через координаты вектора, в произвольном базисе сохраняются. Рассмотрим, как изменится выражение для скалярного произведения, записанное через их координаты в произвольном базисе. Итак, пусть 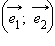 – произвольный базис,  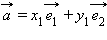и 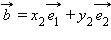 – любые два вектора. Рассмотрим скалярное произведение этих векторов и преобразуем его, используя ранее доказанные свойства:

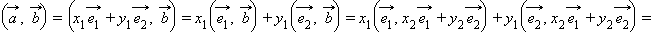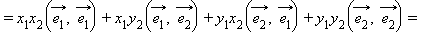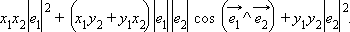Таким образом, для вычисления скалярного произведения двух векторов в произвольном базисе, кроме их координат, надо знать модули базисных векторов и угол между ними. Очевидно, что если базис ортонормирован, то 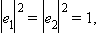 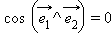 и мы получим известную формулу для скалярного произведения в ортогональной декартовой системе координат.

Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства (см., например, доказательство теоремы 11.10). Часто одно и то же множество приходится рассматривать в разных координатах. Одна и та же точка в различных системах имеет, очевидно, различные координаты. Множество точек (в частности, прямая, окружность) в разных системах координат задается различными уравнениями. Выясним, как преобразуются координаты точек плоскости при переходе от одной координатной системы к другой. Ограничимся случаем ортогональных систем.

Пусть на плоскости заданы две прямоугольные системы координат: 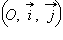 и 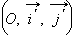 (см. рис. 11.3.2).

2

Рисунок 11.3.2

Первую систему с началом в точке O и базисными векторами  и 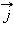 назовем старой, вторую, с началом в точке 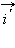O' и базисными векторами  и 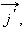 – новой. Положение новой системы относительно старой будем считать известным: пусть точка 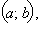O' в старой системе имеет координаты  а вектор  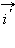образует с вектором 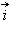угол α, который отсчитывается в направлении против движения часовой стрелки от направления, задаваемого вектором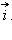

Рассмотрим произвольную точку M. Обозначим ее координаты в старой системе через (x, y), в новой – через (x', y'). Установим связь между старыми и новыми координатами точки M. Из рис. 11.3.2 по правилу треугольника имеем
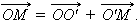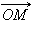Разложим векторы  и 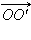 по базису  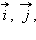а вектор  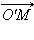– по базису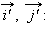
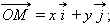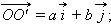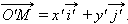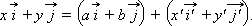Равенство перепишется в виде:
Новые базисные векторы  и 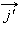 можно разложить по старым базисным векторам  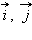следующим образом:
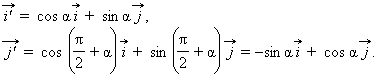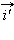Подставив найденные выражения для  и 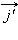 в формулу, получим векторное равенство
равносильное двум числовым равенствам:
Эти формулы дают искомое выражение для старых координат через новые координаты x' и y'. Для того чтобы найти выражение для новых координат через старые, достаточно решить систему уравнений относительно неизвестных x' и y'.

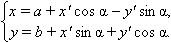Если меняется только начало координат, а направления осей остаются прежними, то, полагая в формулах α = 0, получаем
Эти формулы кратко называют формулами переноса.

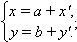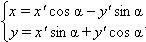Если начало координат остается прежним, а оси поворачиваются на угол α, то, полагая в формулах a = b = 0, получим
Эти формулы называются формулами поворота.