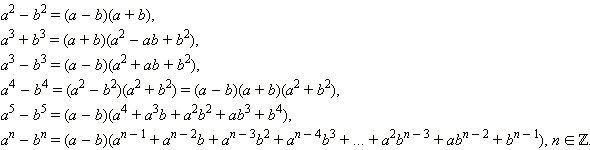Глава 3. Решение уравнений и неравенств
3.1.
3.1.2.
Изучение приёмов преобразования уравнений начнём с обсуждения того, как можно разлагать на множители выражения, входящие в данное уравнение. Вообще представление уравнения f (x) = g (x) в виде
|
|
F1 (x) · F2 (x) · ... · Fn (x) = 0, |
(5)
|
где выражения Fk (x), k = 1, ..., n «проще» функций f (x) и g (x), представляет собой несомненное продвижение в решении уравнения. В самом деле, представление вида (5) позволяет сразу приравнивать множители Fk (x) нулю и решать более простые уравнения. Представление уравнения (1) в виде (5) иногда называют факторизованным видом уравнения (1) (от английского слова «factor» – множитель).
Перечислим теперь некоторые наиболее распространённые приёмы разложения многочленов, как наиболее простых алгебраических функций, на множители.
1. Вынесение общего множителя за скобку
В том случае, когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена.
Пример 1Разложить на множители многочлен x5 – 2x3 + x2.
Каждое слагаемое этого многочлена содержит множитель x2. Вынесем его за скобку и получим ответ: x5 – 2x3 + x2 = x2(x3 – 2x + 1).
|
2. Применение формул сокращённого умножения
Формулы сокращения довольно эффективно применяются при разложении многочлена на множители. Полезно помнить следующие формулы:
Пример 2Разложить на множители многочлен (x – 2)4 – (3x + 1)4.
Разложим разность четвёртых степеней по формуле, приведённой выше:
|
3. Применение выделения полного квадрата
Без преувеличения можно сказать, что метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов. Поясним сказанное на примере.
Пример 3Разложить на множители многочлен x4 + 4x2 – 1.
Имеем 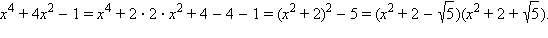
|
4. Группировка
Метод группировки слагаемых, как правило, применяется совместно с другими методами разложения на множители и чаще всего с методом вынесения за скобки. Суть метода состоит в том, что все слагаемые данного многочлена перегруппировываются таким образом, чтобы в каждой группе, возможно после вынесения общего множителя за скобки, образовалось бы одно и то же выражение. Это выражение можно также вынести за скобки как общий для всех групп множитель.
5. Метод неопределённых коэффициентов
Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной.
Теоретической основой метода являются следующие утверждения.
- Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
- Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
- Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.
Для доказательства второго утверждения вспомним, как выглядит график степенной функции с нечетной целой степенью (§ 2.2.5). Действительно, из его вида следует, что значение многочлена имеет разные знаки при x → +∞ и x → –∞. Многочлен степени n – непрерывная функция, значит, найдется хотя бы одна точка, в которой график этой функции пересечет ось Ox.
Пример 4Разложить на множители многочлен 3x3 – x2 – 3x + 1.
Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax2 + bx + c такие, что справедливо равенство
| 3x3 – x2 – 3x + 1 = (x – p)(ax2 + bx + c) = ax3 + (b – ap)x2 + (c – bp)x – pc. |
Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырёх уравнений для определения четырёх неизвестных коэффициентов:
Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1.
Итак, многочлен 3x3 – x2 – 3x + 1 разлагается на множители:
| 3x3 – x2 – 3x + 1 = (x – 1)(3x2 + 2x – 1). |
|
6. Теорема о корнях многочлена
Разложение многочлена на множители иногда удаётся провести, если один из его корней угадан с помощью теоремы о рациональных корнях, доказанной в § 2.1.4. После того, как корень x = α угадан, многочлен Pn (x) представим в виде Pn (x) = (x – α) · Pn – 1 (x), где Pn – 1 (x) − многочлен степени на 1 меньше, чем Pn (x).
Пример 5Разложить на множители многочлен x3 – 5x2 – 2x + 16.
Данный многочлен имеет целые коэффициенты. По следствию теоремы о рациональных корнях (см. § 2.1.4) если целое число является корнем этого многочлена, то оно является делителем числа 16, то есть если у данного многочлена есть целые корни, то это могут быть только числа ±1, ±2, ±4, ±8, ±16.
Проверкой убеждаемся, что число 2 является корнем этого многочлена, то есть
| x3 – 5x2 – 2x + 16 = (x – 2) · Q (x),
|
где Q (x) − многочлен второй степени. Следовательно, исходный многочлен разлагается на множители, один из которых ( x – 2).
|
7. Разложение относительно параметра
Суть этого метода легче всего понять на примере.
Пример 6Разложить на множители многочлен x4 – 10x2 – x + 20.
Преобразуем данный многочлен:
| x4 – 10x2 – x + 20 = x4 – 5 · 2x2 – x + 25 – 5 = 25 – 5(1 + 2x2) + x4 – x |
Рассмотрим теперь многочлен a2 – a(1 + 2x2) + x4 – x, который при a = 5 совпадает с данным. Полученный многочлен является квадратным, его корни легко найти по теореме Виета:
| a2 – a(1 + 2x2) + x4 – x = a2 – a(1 + 2x2) + x(x3 – 1) = a2 – a(1 + 2x2) + x(x – 1)(x2 + x + 1). |
Следовательно, a1 = x(x – 1), a2 = x2 + x + 1. Значит, исходный многочлен разлагается на множители a2 – a(1 + 2x2) + x4 – x = (a – (x2 – x))(a – (x2 + x + 1)). Вернемся к многочлену, данному в условии задачи, подставив a = 5. Получим:
| x4 – 10x2 + x + 20 = (5 – x2 + x)(5 – x2 – x – 1) = (x2 – x – 5)(x2 + x – 4). |
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".