 |
 |
Рассмотрим точки
|
|
|
| Чертеж 9.4.1. Расстояние между точками
|
Проведем через точки 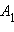 и
и 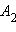 прямые, параллельные оси
прямые, параллельные оси 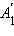 и
и 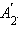 Заметим, что поскольку эти точки лежат в плоскости
Заметим, что поскольку эти точки лежат в плоскости 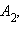 параллельную плоскости
параллельную плоскости 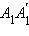 в точке
в точке 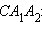
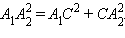 Очевидно, что отрезки
Очевидно, что отрезки 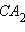 и
и 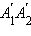 равны, а согласно теореме Пифагора на плоскости
равны, а согласно теореме Пифагора на плоскости 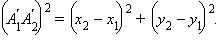 Поскольку длина отрезка
Поскольку длина отрезка 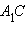 равна
равна 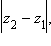 то окончательно имеем
то окончательно имеем 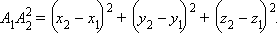
Если же окажется, что отрезок
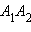 параллелен оси
параллелен оси 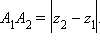 Но тот же результат дает полученная формула, так как в этом случае
Но тот же результат дает полученная формула, так как в этом случае 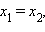
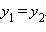
Итак, доказана следующая

Расстояние между точками
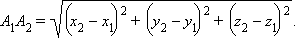 |

Вектор, конец которого совпадает с данной точкой, называется радиус-вектором данной точки.
|
|
|
| Чертеж 9.4.2 |
Рассмотрим некоторую точку
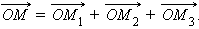 |
По определению координаты точки 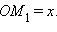 Значит,
Значит, 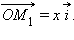 Совершенно аналогично
Совершенно аналогично 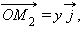
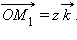 Получается, что
Получается, что 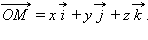 Тем самым доказана следующая
Тем самым доказана следующая

Координаты любой точки равны соответствующим координатам ее радиус-вектора.
Рассмотрим теперь две точки 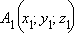 и
и 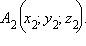 По только что доказанному,
По только что доказанному, 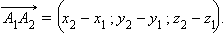 Итак, каждая координата вектора равна разности соответствующих координат его конца и начала. Но длина вектора
Итак, каждая координата вектора равна разности соответствующих координат его конца и начала. Но длина вектора 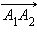 по определению равна длине отрезка
по определению равна длине отрезка 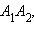 а длина этого отрезка есть расстояние между точками
а длина этого отрезка есть расстояние между точками
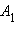 и
и 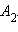 Значит,
Значит,
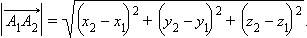 |
 |
 |
 |

