 |
 |

Многогранник, у которого одна грань, называемая основанием, – многоугольник, а другие грани – треугольники с общей вершиной, называется пирамидой.
Грани, отличные от основания, называются боковыми. Общая вершина боковых граней называется вершиной пирамиды.
Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. Обозначая пирамиду, сначала называют ее вершину, а затем – вершины основания.
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой

Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.
Сечение пирамиды плоскостью, проходящей через вершину и диагональ основания, называется диагональным сечением.

Если все боковые ребра пирамиды равны, то ее высота проходит через центр круга, описанного вокруг основания.

Если все боковые грани пирамиды одинаково наклонены к плоскости основания, а высота проходит внутри пирамиды, то высота проходит через центр вписанного в основание пирамиды круга.

Если все боковые грани наклонены к плоскости основания под одинаковым углом
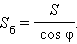 |

Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды.

Для правильной пирамиды справедливы формулы:
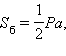 где
где 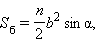 где
где

Если пирамиду пересечь плоскостью, параллельной плоскости основания, (чертеж 4.7.3), то:
|
|
|
| Чертеж 4.7.3 |
боковые ребра и высота делятся этой плоскостью на пропорциональные отрезки в отношении
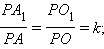 |
площади сечения и основания пирамиды относятся как квадраты их расстояний до вершины пирамиды:
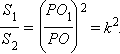 |
 |
 |
 |

