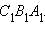Глава 4. Многогранники
4.6. Параллелепипед
Теорема 4.8.
Каждый параллелепипед имеет центр симметрии.
Пусть O – середина диагонали BD1 параллелепипеда ABCDA1B1C1D1 (чертеже 4.6.1). Докажем, что O – центр симметрии всего параллелепипеда. Поскольку каждое диагональное сечение параллелепипеда – параллелограмм с центром O, то для каждой вершины параллелепипеда найдется другая вершина, симметричная ей относительно точки O. Следовательно O – центр симметрии параллелепипеда.
|
Следствие 4.1.
Противоположные грани любого параллелепипеда равны и параллельны.
Определение 4.8. Прямоугольным называется параллелепипед, все грани которого прямоугольники.
Прямоугольный параллелепипед с равными ребрами называется кубом.
Три ребра, выходящие из одной вершины прямоугольного параллелепипеда называются его измерениями (длиной, шириной, высотой).
Теорема 4.9.
Квадрат диагонали прямоугольного параллелепипеда равняется сумме квадратов его измерений:
На чертеже 4.6.2 показан прямоугольный параллелепипед ABCDA1B1C1D1. По теореме Пифагора имеем:
|
Заметим, что если ребро куба равно a, а его диагональ равна d, то 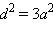 и
и 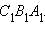
Легко заметить, что все диагонали прямоугольного параллелепипеда равны.


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".





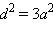 и
и