Глава 4. Многогранники
4.2. Изображение многоугольников и многогранников
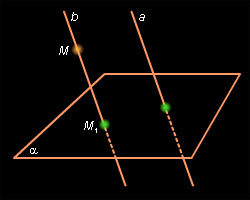
Допустим, что в пространстве задана произвольная плоскость α и пересекающая ее прямая a. Выберем в пространстве произвольную точку M и проведем через нее прямую b, параллельную a.
Определение 4.3.
Точка пересечения M1 прямой b с плоскостью a называется параллельной проекцией точки M на эту плоскость. Плоскость α называется плоскостью проектирования, а прямая a – направлением проектирования.
 1
|
| Рисунок 4.2.1
|
Определение 4.4.
Пусть в пространстве задана некоторая фигура K. Отображение, ставящее в соответствие каждой точке M фигуры K ее параллельную проекцию – точку M1 на плоскость α в направлении a, называется параллельным проектированием (на плоскость α в направлении a). Множество точек M1 называется параллельной проекцией фигуры K на плоскость α в направлении a.
Параллельное проектирование применяется для изображения пространственных фигур на плоскости и обладает следующими свойствами (здесь мы предполагаем, что направление проектирования не параллельно рассматриваемым отрезкам и прямым; в противном случае проекцией будет являться точка).
-
Проекцией прямой является прямая, проекция отрезка есть отрезок.
-
Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой.
-
Длины проекций параллельных отрезков, а также длины проекций отрезков, лежащих на одной прямой, пропорциональны длинам самих этих отрезков.
Изображением данного треугольника может служить любой треугольник.
Для изображения плоского многоугольника выделяют в нем вершины A1, A2, A3. Затем строят изображение треугольника A1A2A3 в виде произвольного треугольника. Изображение остальных вершин многоугольника строится однозначно с использованием свойств параллельного проектирования.
Из приведенного утверждения следует, что изображением данного треугольника может служить треугольник, подобный любому треугольнику. В частности, любой треугольник можно спроектировать в правильный треугольник, то есть правильный треугольник может служить проекцией любого треугольника.
При изображении многогранников полезно следующее утверждение.
Теорема 4.1. Теорема Польке – Шварца.
Изображением данного
тетраэдра может служить любой четырехугольник с проведенными в нем диагоналями (не обязательно выпуклый).
Для изображения многогранника выделяют в нем четыре вершины A1, A2, A3, A4. Затем строят изображение тетраэдра A1A2A3A4 в виде произвольного четырехугольника с проведенными в нем диагоналями. Изображение остальных вершин многогранника строится однозначно с использованием свойств параллельного проектирования.


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".










