 |
 |
Предъявим теперь многогранники каждого вида, доказывая тем самым их существование.
Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр – правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра. Очевидно, что тетраэдр с заданной длиной ребра единственен. Все остальные тетраэдры подобны ему и определяются длиной ребра, что следует из теоремы 8.1.
|
|
|
| Чертеж 8.2.1 |
Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все грани которого – квадраты, и из каждой вершины выходит три ребра.
|
|
|
| Чертеж 8.2.2 |
Октаэдр (okto – восемь). Это правильный многогранник, все грани которого – правильные треугольники и к каждой вершине прилегают четыре грани. Покажем, что этот многогранник имеет восемь граней, указав способ его построения.
|
|
|
| Чертеж 8.2.3 |
Рассмотрим квадрат
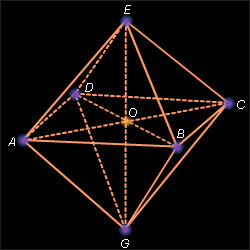
|
| Рисунок 8.2.1 |
Чтобы это доказать, нам остается проверить, что у него равны все двугранные углы. Действительно, пусть
Отметим интересный факт, связанный с гексаэдром (кубом) и октаэдром. Куб имеет 6 граней, 12 ребер и 8 вершин, а октаэдр – 8 граней, 12 ребер и 6 вершин. То есть число граней одного многогранника равно числу вершин другого и наоборот. Как говорят, куб и гексаэдр являются двойственными друг к другу. Это также проявляется в том, что если взять куб и построить многогранник с вершинами в центрах его граней, то, как несложно убедиться, получится октаэдр. Верно и обратное – центры граней октаэдра служат вершинами куба. В этом-то и состоит двойственность октаэдра и куба (рис. 8.2.2).
Несложно сообразить, что если взять центры граней правильного тетраэдра, то мы вновь получим правильный тетраэдр (рис. 8.2.3). Таким образом, тетраэдр двойственен самому себе.
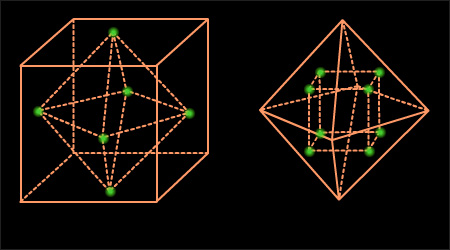
|
| Рисунок 8.2.2 |
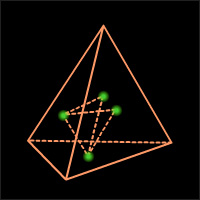
|
| Рисунок 8.2.3 |
 |
 |
 |


| Starmix |
| starmix |
| imperiatools.ru |