Глава 3. Перпендикулярность прямых и плоскостей
3.1. Угол между двумя скрещивающимися прямыми
С появлением в стереометрии скрещивающихся прямых возникает вопрос: как определить угол между двумя скрещивающимися прямыми?
Пусть прямые a и b скрещивающиеся (чертеж 3.1.1). Выберем на прямой a произвольную точку A. Проведем через нее прямую b' || b. Угол между прямыми a и b' по теореме 2.10 равен углу между скрещивающимися прямыми a и b. Ясно, что величина этого угла не зависит от выбора точки A. Действительно, выберем на прямой a точку A1 ≠ A и проведем через нее прямую b1' || b. Поскольку b' || b и b1' || b, то b1' || b'. Прямые b' и b1' образуют с прямой a одинаковые углы.
Определение 3.1. Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Определение 3.2.
Две прямые в пространстве называются перпендикулярными, если они образуют прямой угол. На чертеже 3.1.2 изображен куб ABCDA1B1C1D1. Скрещивающиеся прямые A1D1 и CD перпендикулярны. Действительно, A1D1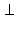 
C1D1, а C1D1 || CD.
Назовем еще несколько пар скрещивающихся перпендикулярных прямых: A1D1 и AB, A1B1 и BC, A1B1 и AD, B1C1 и AB.
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".
