Задачи с решениями

Анализ. Пусть ΔABC – треугольник, который требуется построить; пусть AB = c – данная по условию сторона, AD = a и BE = b – его медианы, M – точка их пересечения.

Известно, что медианы, пересекаясь, делят друг друга в отношении 2:1 считая от вершины. Значит, 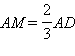 и 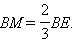  Таким образом, стороны треугольника ΔABM известны и его можно построить.

Построение.

Построим треугольник ABM по трем сторонам.

Продолжим отрезок AM на величину 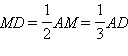и найдем точку D; продолжим отрезок BM на величину 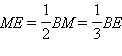и найдем точку E.

Проведем лучи AE и BD и найдем точку C их пересечения. Треугольник ABC искомый.

Доказательство. В треугольнике ABC AB, BE и AD – данные отрезки. Проведем отрезок DF || BE. Поскольку 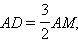  то 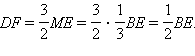  Значит, DF – средняя линия треугольника CBE и D – середина отрезка BC. Аналогично доказывается, что E – середина отрезка AC.