Задачи с решениями

Построить трапецию по основаниям и боковым сторонам.

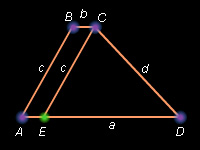
Анализ. Пусть трапеция ABCD имеет основания AD = a, BC = b и боковые стороны AB = c, CD = d (см. рисунок). Проведем отрезок CE || AB. В ΔCDE известны три стороны: CD = d, CE = c, DE = a – b. Отсюда следует построение.

Построение. Строим ΔCDE по трем сторонам: d, c и a – b. Затем продлеваем отрезок DE на AE = b и получаем вершину трапеции A. Далее проводим из т. C прямую, параллельную AD, и откладываем отрезок CB = b. B – четвертая вершина трапеции.

2 из 6