Построение фигур Задачи с решениями
Задачи с решениями

Из данной точки A, лежащей вне данной окружности w (O, r), провести касательную к ней.
Решение
Анализ. Пусть w (O, r) – данная окружность и A – данная точка вне нее. Пусть построена касательная AB к окружности (см. первый рисунок). По свойству касательной OB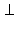 AB и ΔOBA – прямоугольный с заданной гипотенузой OA. Но в силу следствия 6.2 мы знаем, что множество вершин прямоугольных треугольников с заданной гипотенузой, противолежащих ей, образуют окружность с диаметром, совпадающим с гипотенузой. Отсюда способ построения.
AB и ΔOBA – прямоугольный с заданной гипотенузой OA. Но в силу следствия 6.2 мы знаем, что множество вершин прямоугольных треугольников с заданной гипотенузой, противолежащих ей, образуют окружность с диаметром, совпадающим с гипотенузой. Отсюда способ построения.
Построение. Соединим центр окружности O с точкой A (см. второй рисунок). Построим середину C отрезка OA. Проведем окружность радиуса OC с центром в точке C. Пусть B и D – точки пересечения построенной окружности с данной. Проведем прямые AB и AD. Это искомые касательные.
Доказательство. Действительно, по построению углы OBA и ODA – вписанные в окружность w (C, CO) и опираются на диаметр OA этой окружности. По следствию 7.2 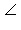 OBA =
OBA = 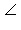 ODA = 90°. Кроме того, по построению точки B и D лежат на данной окружности w (O, r). Следовательно, по определению AB и AD – касательные к w (O, r).
ODA = 90°. Кроме того, по построению точки B и D лежат на данной окружности w (O, r). Следовательно, по определению AB и AD – касательные к w (O, r).
 1 из 6
1 из 6
 |
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


 Задачи с решениями
Задачи с решениями

![]() AB
AB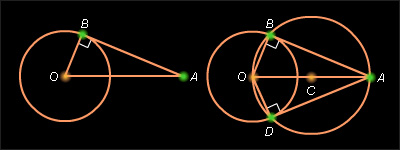
![]() OBA =
OBA = ![]() ODA = 90°
ODA = 90° 1 из 6
1 из 6
