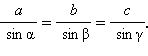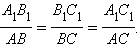Глава 5. Решение треугольников
5.2. Соотношения между сторонами и углами произвольного треугольника
Под косинусом тупого угла α (90° < α < 180°) будем понимать значение косинуса смежного с ним угла, взятого со знаком минус. Косинус прямого угла будем считать равным 0.
Под синусом тупого угла будем понимать синус смежного угла. Синус прямого угла будем считать равным 1.
Из этих определений следует, что для любых углов, таких, что 0 < α < 180° справедливы равенства
| sin α = sin (180° – α) и cos α = –cos (180° – α).
|
Действительно, если α = 90°, то имеем верные равенства.
| sin 90° = sin (180° – 90°) и cos 90° = 0 = –cos (180° – 90°).
|
Если α – острый угол, то 180° – α = β, 90° < α < 180° – тупой угол. Тогда по определению
| sin β = sin (180° – β) или sin (180° – α) = sin (180° – (180° – α)) = sin α.
|
| cos β = –cos (180° – β) или cos (180° – α) = –cos (180° – (180° – α)) = –cos α.
|
Отсюда получаем cos α = cos (180° – α).
Наконец, если α (90° < α < 180°) – тупой угол, то равенства видны по определению.
Теорема 5.3. Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Пусть угол α – между двумя сторонами AB и AC треугольника ABC равен 90°. Тогда треугольник ABC прямоугольный и по теореме Пифагора имеем
Но с другой стороны, так как cos 90° = 0
| AB2 + AC2 = AB2 + AC2 – 2AB · AC cos 90° = BC2.
|
Теорема верна.
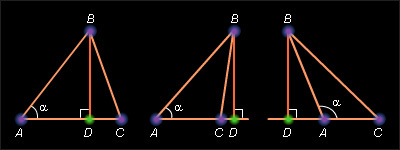
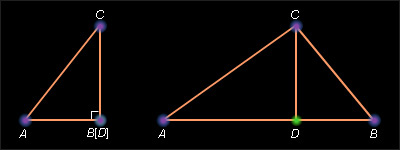
На рис. 5.2.1 показаны три возможных случая, связанных с величиной угла α между известными сторонами. В первых двух случаях угол α – острый, в третьем – тупой. Пусть ABC – данный треугольник. Докажем, что BC2 = AB2 + AC2 – 2AB · AC cos α. Опустим из вершины B высоту BD на прямую (AC). Рассмотрим два возможных случая.
-
Пусть угол α – острый. Тогда, либо точка D лежит между точками A и C, либо точка C – между точками A и D. Поэтому справедливы следующие равенства: AB2 = AD2 + BD2; BC2 = CD2 + BD2, AD = AB cos α, CD = |AC – AD|. Из первых двух равенств, исключая BD2, получим BC2 = AB2 + CD2 – AD2. Подставляя из последнего равенства выражение для CD, имеем: BC2 = AB2 + (|AC – AD|)2 – AD2 = AB2 + AC2 – 2AC · AD. С учетом третьего равенства окончательно получаем требуемое равенство: BC2 = AB2 + AC2 – 2AB · AC cos α.
-
Пусть угол α – тупой. Тогда точка A лежит между точками D и C. Поэтому справедливы равенства: AB2 = AD2 + BD2, BC2 = CD2 + BD2, AD = AB cos(180° – α), CD = AC + AD. Имеем: BC2 = AB2 + CD2 – AD2. С учетом последнего равенства BC2 = AB2 + (AC + AD)2 – AD2 = AB2 + AC2 + 2AC · AD = AB2 + AC2 + 2AB · AC · cos (180° – α).
Так как угол α – тупой , то cos α = –cos (180° – α) и, с учетом этого, окончательно получаем BC2 = AB2 + AC2 – 2AB · AC cos α. Теорема доказана.
 1
|
| Рисунок 5.2.1. К доказательству теоремы косинусов
|
 2
|
| Рисунок 5.2.2. К доказательству теоремы косинусов
|
|
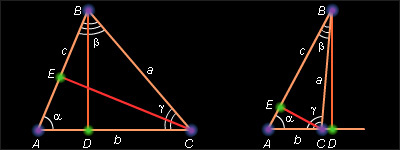
Теорема 5.4. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов, т.е.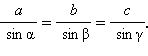 
Пусть ABC – треугольник со сторонами a, b, c и соответственно противолежащими им углами α, β, γ. Докажем, что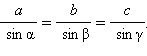 
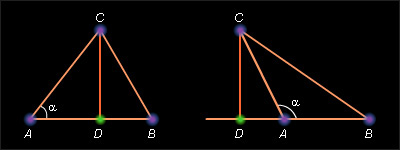
Опустим из вершины B высоту BD на прямую (AC).
-
Пусть все углы Δ ABC острые. Тогда BD = a sin γ из прямоугольного треугольника BCD. Аналогично из треугольника ABD BD = c sin α. Приравнивая правые части, получаем a sin γ = c sin α или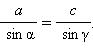 
Аналогично, если опустить высоту CE из вершины C на прямую (AB), получим CE = b sin α из Δ ACE, CE = a sin β из Δ BCE. И, сравнивая эти равенства, имеем 
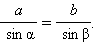Окончательно из полученных равенств имеем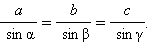 
-
Пусть один из углов (например, γ) тупой. Тогда BD = a sin(180° – γ ) = a sin γ из Δ BCD, BD = c sin α из Δ ABD. Отсюда a sin γ = c sin α или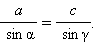 
Далее, опуская высоту CE из вершины C на прямую (AB) и рассуждая аналогично пункту 1, получим 
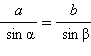и, окончательно, 
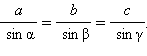Теорема доказана.
 3
|
| Рисунок 5.2.3. К доказательству теоремы синусов
|
|
Следствие 5.1.
Пусть даны два треугольника ABC и A1B1C1 и углы при вершинах A, B и C одного треугольника равны углам при вершинах A1, B1, C1 соответственно, другого треугольника. Тогда отношения длин сторон этих треугольников, лежащих против равных углов равны, то есть
Действительно из Δ ABC по теореме синусов имеем
Аналогично из Δ A1B1C1 получим
Деля входящие во второе равенство выражения на соответствующие выражения из первого равенства и учитывая, что синусы равных углов равны получим искомое равенство.
|
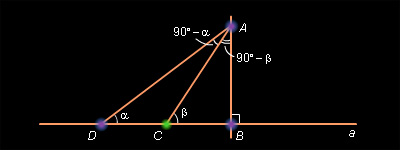
Лемма 5.1.
Пусть α и β – угловые величины двух острых углов, причем α < β. Тогда sin α < sin β
 4
|
| Рисунок 5.2.4
|
Отложим от луча AB в одну полуплоскость углы BAC и BAD так, что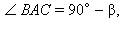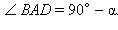  
Точки B, C, D лежат на прямой a, которая перпендикулярна лучу AB. Так как 
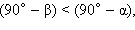то луч AC лежит между сторонами угла BAD, следовательно, точка C лежит между точками B и D и BC < BD. Отрезки BC и BD являются проекциями наклонных AC и AD на прямую a, соответственно, поэтому, по свойству наклонных (см. параграф 5.1) AD > AC. Треугольники ABC и ABD прямоугольные (
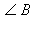равен 90° по условию), поэтому  
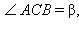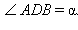По определению
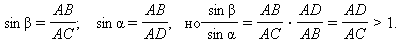Отсюда  |
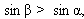что и требовалось доказать.
Заметим, что, если α – острый угол, то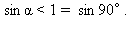 
|
 5
|
| Рисунок 5.2.5. К следствию 5.2
|
Следствие 5.2.
В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Если все углы треугольника – острые, то этот факт следует из результата леммы 5.1 и теоремы 5.4. Если же один из углов треугольника, например, для определенности γ – тупой, то γ = 180° – (α + β), но sin (180° – (α + β)) = sin (α + β) и по лемме 5.2 sin (α + β) = sin γ > sin α и sin γ > sin β. Bторое утверждение следует из теоремы 5.4.
|
Теорема 5.5. Неравенство треугольника.
Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей.
Пусть A, B, C – три данные точки. Если две точки из трех или все три совпадают, то утверждение теоремы очевидно. Если все три точки различны, но лежат на одной прямой, одна из них лежит между двумя другими без ограничения общности, например, B. Тогда AB + BC = AC. Отсюда AB < AC < AC + BC, BC < AC < AC +BC, AC = AB + BC и утверждение теоремы верно.
Пусть точки A, B и C не лежат на одной прямой. Докажем, что AB < AC + BC. Опустим перпендикуляр CD на прямую AB.. Точки A, B, D лежат на данной прямой и по доказанному AB ≤ AD +BD. Но AD < AC и BD < BC по построению и свойству наклонной. Отсюда AB < AC + BC. Теорема доказана.
 6
|
| Рисунок 5.2.6. Неравенство треугольника
|
|
Следствие 5.3.
В любом треугольнике каждая сторона меньше суммы двух других сторон.
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".
