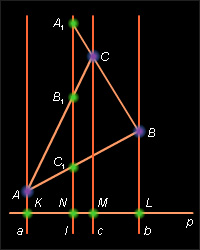
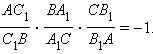Необходимость. Пусть прямая l пересекает прямые AB, BC, AC соответственно в точках C1, A1 и B1 (рис. 14.2.1). Проведем произвольную прямую P, пересекающую прямую l в точке N, а через точки A, B и C соответственно прямые a, b и c, параллельные прямой l и пересекающие p в точках K, L, M. По теореме о пропорциональных отрезках
Перемножая равенства и учитывая, что
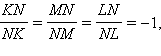
получаем искомое равенство.
 1
|
| Рисунок 14.2.1
|
Достаточность. Пусть дан треугольник ABC, точки 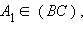
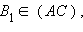
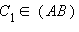 и пусть выполнено необходимое условие. Докажем, что точки A1, B1 и C1 лежат на одной прямой. Проведем прямую через заданные две точки A1 и B1. Эта прямая пересекает прямую AB в некоторой точке C'.
и пусть выполнено необходимое условие. Докажем, что точки A1, B1 и C1 лежат на одной прямой. Проведем прямую через заданные две точки A1 и B1. Эта прямая пересекает прямую AB в некоторой точке C'.
Действительно, если допустить противное, а именно, что прямая A1B1'║(AB), то из подобия треугольников CA1B1 и CBA следует, что 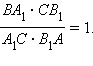 С учетом необходимого условия получим, что
С учетом необходимого условия получим, что 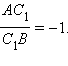 Но такой точки не может существовать, и мы пришли к противоречию. По условию имеем:
Но такой точки не может существовать, и мы пришли к противоречию. По условию имеем: 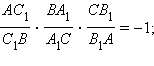 с другой стороны, в силу необходимого условия справедливо равенство
с другой стороны, в силу необходимого условия справедливо равенство 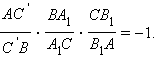 Откуда получаем
Откуда получаем 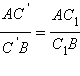 и приходим к выводу, как и в случае доказательства обобщенной теоремы Чевы, что точки C1 и C' совпадают.
и приходим к выводу, как и в случае доказательства обобщенной теоремы Чевы, что точки C1 и C' совпадают.



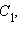
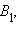
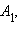 на, соответственно, прямых
на, соответственно, прямых 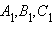 лежат на одной прямой тогда и только тогда, когда выполняется равенство
лежат на одной прямой тогда и только тогда, когда выполняется равенство