Глава 12. Преобразования
12.4. Симметрия и поворот
Точки X и
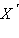 называются симметричными относительно прямой a, и каждая из них – симметричной другой, если a является серединным перпендикуляром отрезка
называются симметричными относительно прямой a, и каждая из них – симметричной другой, если a является серединным перпендикуляром отрезка
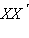 (см. рис. 12.4.1). Очевидно, что если дана прямая a, то каждой точке X соответствует единственная точка
(см. рис. 12.4.1). Очевидно, что если дана прямая a, то каждой точке X соответствует единственная точка
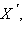 симметричная относительно a. Кроме того, множеством неподвижных точек преобразования симметрии относительно прямой a является эта прямая a.
симметричная относительно a. Кроме того, множеством неподвижных точек преобразования симметрии относительно прямой a является эта прямая a.
Преобразованием симметрии относительно прямой a (или осевой симметрией с осью a) называется такое преобразование фигуры F (см. рис. 12.4.2), при котором каждой точке данной фигуры сопоставляется точка, симметричная ей относительно прямой a. Обозначим
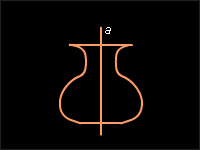
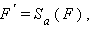 a – ее ось симметрии. Фигура называется симметричной относительно прямой a, если фигура симметрична сама себе (см. рис. 12.4.3), то есть
a – ее ось симметрии. Фигура называется симметричной относительно прямой a, если фигура симметрична сама себе (см. рис. 12.4.3), то есть
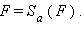
Замечание. Поскольку симметричность точек относительно прямой взаимна, то фигуры F и
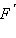 называются симметричными относительно прямой a.
называются симметричными относительно прямой a.
 1
|
| Рисунок 12.4.1. Симметрия точек относительно прямой
|
|
 2
|
| Рисунок 12.4.2. Симметрия треугольников
|
|
 3
|
| Рисунок 12.4.3. Симметрия фигур
|
|
Теорема 12.10.
Преобразование симметрии относительно прямой является движением.
Поворотом фигуры F вокруг центра O на данный угол
φ (0° ≤ φ ≤ 180°) в данном направлении называется такое ее преобразование, при котором каждой точке X  F сопоставляется точка
F сопоставляется точка
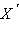 так, что
так, что
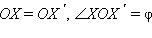 и луч
и луч
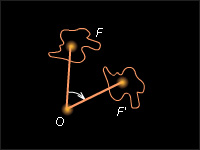
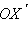 откладывается от луча OX в заданном направлении. Точка O называется центром поворота, а угол φ – углом поворота (рис. 12.4.4). Множеством неподвижных точек преобразования поворота является центр поворота.
откладывается от луча OX в заданном направлении. Точка O называется центром поворота, а угол φ – углом поворота (рис. 12.4.4). Множеством неподвижных точек преобразования поворота является центр поворота.
 4
|
| Рисунок 12.4.4. Поворот фигуры
|
Теорема 12.11.
Поворот является движением.
Пусть при повороте вокруг точки O точкам X и Y сопоставляются точки
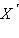 и и
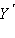 (рис. 12.4.5).
(рис. 12.4.5).
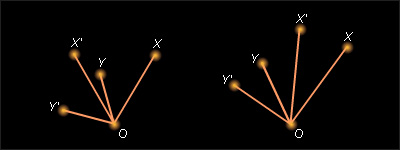 5
|
| Рисунок 12.4.5. К теореме 12.11
|
Очевидно,
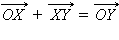 и
и
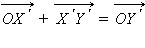 по теореме 11.6. Откуда
по теореме 11.6. Откуда
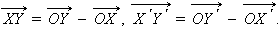 Из этих равенств имеем:
Из этих равенств имеем:
где α = 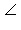 XOY XOY,
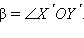
Но по определению поворота
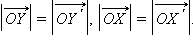
Кроме того,
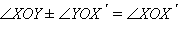
и
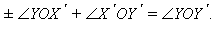
Знаки «+» или «–» выбираются соответственно, если OY лежит между OX и
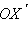
и если OY не лежит между
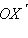
и OX. Но по определению
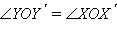
– углу поворота. Отсюда
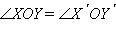
или α = β. В итоге получаем
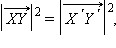
откуда
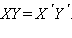
Следовательно, по определению поворот – движение. Теорема доказана.
|
Точки X и
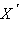 называются симметричными относительно заданной точки O, если
называются симметричными относительно заданной точки O, если
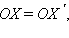 а лучи OX и
а лучи OX и
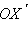 являются дополнительными. Точка O считается симметричной самой себе.
являются дополнительными. Точка O считается симметричной самой себе.
Преобразованием симметрии (или центральной симметрией) относительно точки O называется такое преобразование фигуры F, при котором каждой ее точке X сопоставляется точка
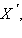 симметричная относительно точки O. Обозначается
симметричная относительно точки O. Обозначается
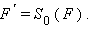 Фигура называется симметричной относительно точки O или центрально-симметричной, если она симметрична сама себе относительно точки O. Точка O называется центром симметрии.
Фигура называется симметричной относительно точки O или центрально-симметричной, если она симметрична сама себе относительно точки O. Точка O называется центром симметрии.
Теорема 12.12.
Центральная симметрия является движением.
Справедливость теоремы следует из того, что центральная симметрия есть поворот на 180°, и теоремы 12.11.
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


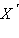 называются симметричными относительно прямой
называются симметричными относительно прямой 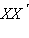 (см. рис. 12.4.1). Очевидно, что если дана прямая
(см. рис. 12.4.1). Очевидно, что если дана прямая 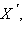 симметричная относительно
симметричная относительно 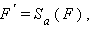
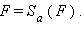
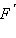 называются симметричными относительно прямой
называются симметричными относительно прямой 
![]() F
F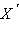 так, что
так, что
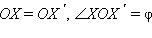 и луч
и луч
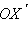 откладывается от луча
откладывается от луча 

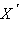 называются симметричными относительно заданной точки
называются симметричными относительно заданной точки 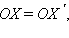 а лучи
а лучи 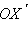 являются дополнительными. Точка
являются дополнительными. Точка 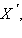 симметричная относительно точки
симметричная относительно точки 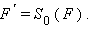 Фигура называется симметричной относительно точки
Фигура называется симметричной относительно точки 




