 |
 |
Суммой векторов 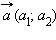 и
и 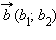 называется вектор
называется вектор 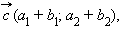
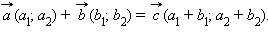 Для любых векторов
Для любых векторов 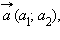
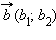 справедливы равенства
справедливы равенства
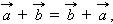 |
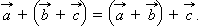 |

Каковы бы ни были три точки 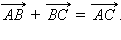
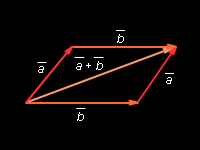
Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
|
| Рисунок 11.2.3. Правило параллелограмма
|
Разностью векторов 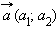 и
и 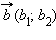 называется такой вектор
называется такой вектор 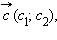 который в сумме с вектором
который в сумме с вектором 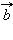 дает вектор
дает вектор 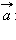
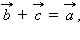 откуда
откуда
Произведением вектора 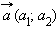 на число
на число 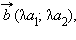 т. е.
т. е. 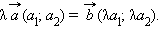
Для любого вектора 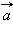 и чисел
и чисел
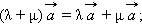 |
Для любых двух векторов 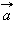 и
и 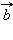 и числа
и числа
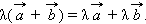 |

Абсолютная величина вектора 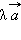 равна
равна 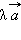 при
при 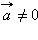 совпадает с направлением вектора
совпадает с направлением вектора 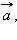 если
если 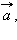 если
если

Для любых отличных от нуля коллинеарных векторов 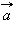 и
и 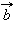 существует такое число
существует такое число 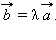

Пусть 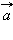 и
и 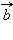 – отличные от нуля неколлинеарные векторы. Любой вектор
– отличные от нуля неколлинеарные векторы. Любой вектор 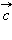 можно единственным образом представить в виде
можно единственным образом представить в виде 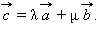
Скалярное произведение векторов.
Скалярным произведением векторов 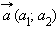 и
и 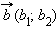 называется число
называется число 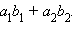 Скалярное произведение векторов
Скалярное произведение векторов 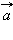 и
и 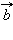 обозначется
обозначется 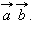
Для любых векторов 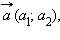
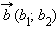 и
и 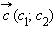 верно:
верно:
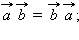
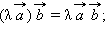
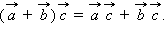

Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Единичные векторы 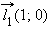 и
и 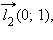 имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.
имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.

Любой ненулевой вектор 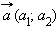 единственным образом можно разложить по координатным векторам, то есть записать в виде
единственным образом можно разложить по координатным векторам, то есть записать в виде 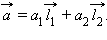
 |
 |
 |

