 |
 |
Введем на плоскости систему координат  где
где 
 через координаты прообраза
через координаты прообраза
|
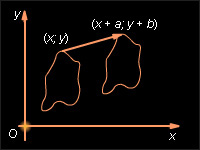
| Рисунок 12.3.1. Парралельный перенос
|

Каковы бы ни были две точки  существует один и только один параллельный перенос, при котором точка
существует один и только один параллельный перенос, при котором точка 

Параллельный перенос есть движение.

Движение, сохраняющее направление, является параллельным переносом.
 |
 |
 |

