Векторы Задачи с решениями
Задачи с решениями

Используя векторы, доказать, что в любом треугольнике медианы пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Решение
Пусть дан треугольник ABC и его медианы AD и BE персекаются в точке O. В соответсвии с задачей 8 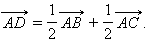 Но точка O лежит на отрезок
Но точка O лежит на отрезок 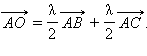
Аналогично, 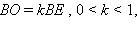
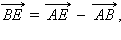
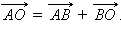 Отсюда
Отсюда 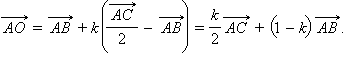 С учетом ранее полученного выражения для
С учетом ранее полученного выражения для 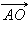 имеем равенство
имеем равенство 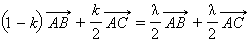 или
или 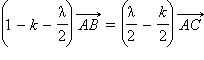 Но
Но 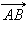 и
и 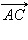 не коллинеарны и равенство возможно лишь при при одновременном выполнении равенств
не коллинеарны и равенство возможно лишь при при одновременном выполнении равенств 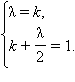 Отсюда
Отсюда 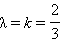 и, следовательно,
и, следовательно, 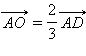 и
и 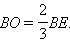 Заменив в рассуждениях медиану BE медианой CF мы снова получим, что эти медианы пересекаются в той точке отрезка AD, которая удалена от точки A на расстояние 2 / 3 от вершины A т. е. в точке O. Таким образом все три медианы пересекаются в одной точке O и при этом
Заменив в рассуждениях медиану BE медианой CF мы снова получим, что эти медианы пересекаются в той точке отрезка AD, которая удалена от точки A на расстояние 2 / 3 от вершины A т. е. в точке O. Таким образом все три медианы пересекаются в одной точке O и при этом 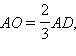
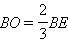 и
и 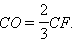
 11 из 25
11 из 25
 |
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


 Задачи с решениями
Задачи с решениями

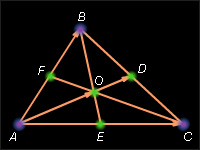
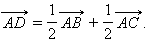 Но точка
Но точка 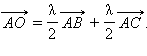
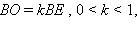
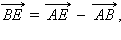
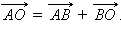 Отсюда
Отсюда 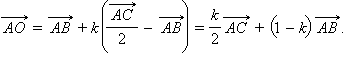 С учетом ранее полученного выражения для
С учетом ранее полученного выражения для 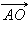 имеем равенство
имеем равенство 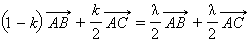 или
или 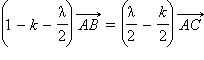 Но
Но 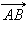 и
и 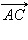 не коллинеарны и равенство возможно лишь при при одновременном выполнении равенств
не коллинеарны и равенство возможно лишь при при одновременном выполнении равенств 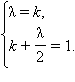 Отсюда
Отсюда 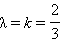 и, следовательно,
и, следовательно, 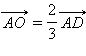 и
и 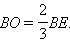 Заменив в рассуждениях медиану
Заменив в рассуждениях медиану 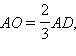
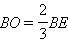 и
и 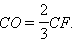
 11 из 25
11 из 25
