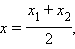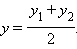Глава 11. Векторы
11.4. Решение задач векторным методом
При решении геометрических задач векторным методом нужно от геометрической постановки задачи перейти к ее векторному описанию. Затем, пользуясь свойствами векторов и операций над ними, найти некоторые векторные соотношения, отражающие данные и условия задачи, из которых можно получить решение задачи. Рассмотрим несколько примеров.
Задача 1. Доказать, что отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям.
 1
|
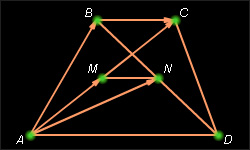
| Рисунок 11.4.1
|
Пусть M и N – середины диагоналей трапеции ABCD (см. рис. 11.4.1). Покажем, что MN || AD. Для этого достаточно показать, что 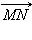 коллинеарен
коллинеарен 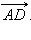
Так как M и N – середины отрезков AC и BD, то
Следовательно,
Но 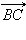 коллинеарен вектору
коллинеарен вектору 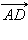 , поэтому
, поэтому 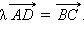 Тогда
Тогда
то есть 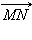 коллинеарен
коллинеарен 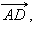 что и требовалось доказать.
что и требовалось доказать.
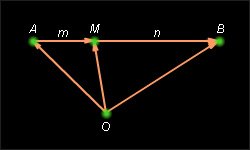
Задача 2. Разделить данный отрезок AB в данном отношении m : n, то есть найти точку M AB, такую, что AM : MB = m : n.
AB, такую, что AM : MB = m : n.
 2
|
| Рисунок 11.4.2
|
Очевидно, что M AB делит отрезок AB в заданном отношении m : n тогда и только тогда, когда
AB делит отрезок AB в заданном отношении m : n тогда и только тогда, когда 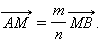 Кроме того,
Кроме того,
Отсюда
Подставляя в исходное соотношение, имеем
откуда находим
В частности, если M – середина отрезка AB, то m = n, и получим
Если точки A и B заданы своими координатами в некоторой декартовой системе координат 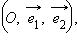 то, используя формулу, можно легко найти координаты точки M в той же системе координат. Векторное равенство равносильно числовым равенствам
то, используя формулу, можно легко найти координаты точки M в той же системе координат. Векторное равенство равносильно числовым равенствам
где 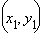 и
и 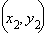 – координаты концов отрезка AB, а x и y – координаты искомой точки M.
– координаты концов отрезка AB, а x и y – координаты искомой точки M.
В частности, когда точка M является серединой отрезка AB, получаем
Таким образом, мы векторным путем получили результаты, полученные нами ранее в § 10.2 (см. теоремы 10.3 и 10.4).


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".



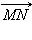 коллинеарен
коллинеарен 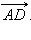
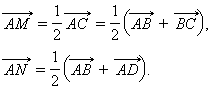
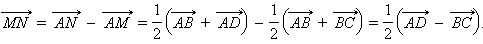
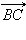 коллинеарен вектору
коллинеарен вектору 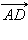 , поэтому
, поэтому 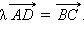 Тогда
Тогда
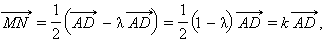
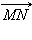 коллинеарен
коллинеарен 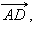 что и требовалось доказать.
что и требовалось доказать.
![]() AB
AB
![]() AB
AB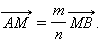 Кроме того,
Кроме того,
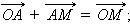
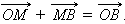
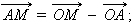
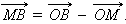
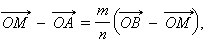
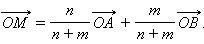
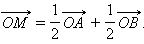
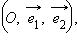 то, используя формулу, можно легко найти координаты точки
то, используя формулу, можно легко найти координаты точки 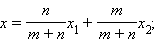
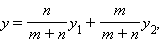
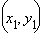 и
и 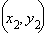 – координаты концов отрезка
– координаты концов отрезка