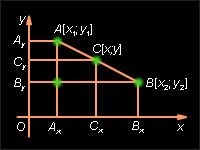
Пусть [AB] – заданный отрезок, где A (x1; y1), B (x2; y2). Предположим x1 ≠ x2, y1 ≠ y2. Тогда прямая AB не параллельна осям координат. Проведем через точки A, C и B прямые, параллельные оси ординат. Они пересекут ось абсцисс в точках 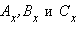 соответственно. По теореме 4.13 имеем
соответственно. По теореме 4.13 имеем 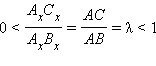 или
или 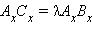 или
или 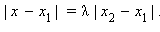 Отсюда либо x – x1 = λ (x2 – x1) или x = x1 + λ (x2 – x1), либо x – x1 = –λ (x2 – x1). Но если C – середина отрезка, то по теореме 10.3
Отсюда либо x – x1 = λ (x2 – x1) или x = x1 + λ (x2 – x1), либо x – x1 = –λ (x2 – x1). Но если C – середина отрезка, то по теореме 10.3 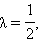
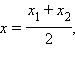 и второе равенство преобразуется к равенству
и второе равенство преобразуется к равенству 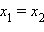 , что противоречит предположению.
, что противоречит предположению.
Если x1 = x2, то x = x1 = x2 и равенство остается верным.
 2
|
| Рисунок 10.2.2
|
Аналогично доказывается, что ордината точки C удовлетворяет равенству y = y1 + λ (y2 – y1). Пусть теперь точка C (x; y) – произвольная точка плоскости, координаты которой удовлетворяют заданным равенствам, где A (x1; y1) и B (x2; y2) – координаты двух разных заданных точек A и B соответственно в плоскости Oxy. Длина отрезка 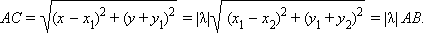 С учетом, что 0 < λ < 1, AC = λ · AB. Длина отрезка
С учетом, что 0 < λ < 1, AC = λ · AB. Длина отрезка 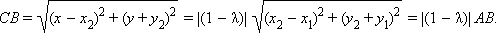 Таким образом AC + CB = λ · AB + (1 – λ) AB = AB. Отсюда на основании аксиомы 1.4 и теоремы 5.5 имеем, что точка C принадлежит отрезку AB. Теорема доказана.
Таким образом AC + CB = λ · AB + (1 – λ) AB = AB. Отсюда на основании аксиомы 1.4 и теоремы 5.5 имеем, что точка C принадлежит отрезку AB. Теорема доказана.




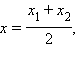
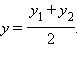

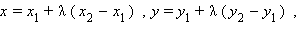 где
где 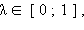 и наоборот, любая точка
и наоборот, любая точка ![]() [0; 1]
[0; 1]



