Глава 11. Векторы
11.5. Векторные уравнения прямой
Положение прямой на плоскости может быть задано одним из следующих способов:
-
прямая l проходит через точку
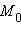 параллельно вектору
параллельно вектору 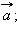
-
прямая l проходит через точки
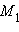 и
и 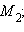
-
прямая l проходит через точку
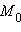 перпендикулярно вектору
перпендикулярно вектору 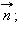
-
прямая l проходит через точку
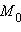 и составляет с вектором
и составляет с вектором 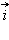 угол α (см. рис. 11.5.1).
угол α (см. рис. 11.5.1).
 1
|
| Рисунок 11.5.1
|
Любой вектор 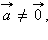 параллельный прямой l, называется направляющим вектором этой прямой. Любой вектор
параллельный прямой l, называется направляющим вектором этой прямой. Любой вектор 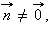 перпендикулярный прямой l, называется нормальным вектором прямой. Если взять на прямой какие-либо две фиксированные точки
перпендикулярный прямой l, называется нормальным вектором прямой. Если взять на прямой какие-либо две фиксированные точки 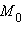 и
и 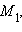 то вектор
то вектор 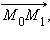 в частности, будет направляющим вектором прямой
в частности, будет направляющим вектором прямой 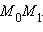
Пусть прямая l задана точкой 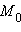 и направляющим вектором
и направляющим вектором 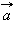 (см. рис. 11.5.2). Пусть M – произвольная точка прямой.
(см. рис. 11.5.2). Пусть M – произвольная точка прямой.
 2
|
| Рисунок 11.5.2
|
|
 3
|
| Рисунок 11.5.3
|
|
Обозначим 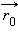 и
и 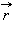 радиус-векторы точек
радиус-векторы точек 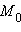 и M соответственно. Вектор
и M соответственно. Вектор 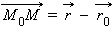 параллелен прямой, и, следовательно, вектору
параллелен прямой, и, следовательно, вектору 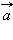 тогда и только тогда, когда M лежит на прямой. Так как
тогда и только тогда, когда M лежит на прямой. Так как 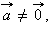 то
то
Переменная t, принимающая различные значения, называется параметром, а уравнение – векторно-параметрическим уравнением прямой.
Если ввести систему координат 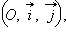 то уравнение можно записать в виде
то уравнение можно записать в виде
где 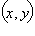 и
и 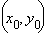 – координаты точек
– координаты точек 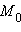 и M, а
и M, а 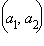 – координаты вектора
– координаты вектора 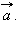 Отсюда следует, что
Отсюда следует, что
Эти уравнения называются параметрическими уравнениями прямой.
Пусть 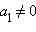 и
и 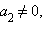 тогда из уравнений следует, что
тогда из уравнений следует, что 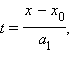
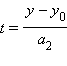 и, окончательно, уравнение
и, окончательно, уравнение 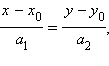 которое называется каноническим уравнением прямой, с направляющим вектором
которое называется каноническим уравнением прямой, с направляющим вектором 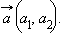
Если 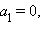 то параметрическое уравнение примет вид
то параметрическое уравнение примет вид
Это уравнение задает прямую, параллельную оси Oy и проходящую через точку 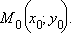 Каноническое уравнение прямой имеет вид
Каноническое уравнение прямой имеет вид 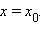 Аналогично, если
Аналогично, если 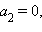 то прямая, задаваемая системой
то прямая, задаваемая системой
проходит через точку 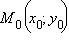 параллельно оси Ox. Ее каноническое уравнение имеет вид
параллельно оси Ox. Ее каноническое уравнение имеет вид 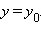
Как было отмечено ранее, направляющим вектором прямой можно выбрать вектор 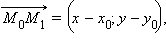 где
где 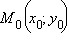 и
и 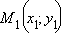 – произвольные две точки прямой. Тогда, подставив координаты вектора
– произвольные две точки прямой. Тогда, подставив координаты вектора 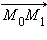 в каноническое уравнение, получим уравнение прямой, проходящей через две заданные точки:
в каноническое уравнение, получим уравнение прямой, проходящей через две заданные точки:
Рассмотрим уравнение прямой, проходящей через две точки 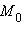 и
и 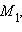 первая из которых лежит на оси Ox и имеет, следовательно, координаты
первая из которых лежит на оси Ox и имеет, следовательно, координаты 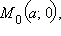 а вторая лежит на оси Oy и имеет координаты
а вторая лежит на оси Oy и имеет координаты 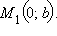 Подставляя их в уравнение, получим
Подставляя их в уравнение, получим
или
Это уравнение называется уравнением прямой в отрезках, так как числа a и b указывают, какие отрезки отсекает прямая на осях координат.
Пусть 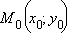 – некоторая точка прямой,
– некоторая точка прямой, 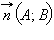 – вектор, перпендикулярный прямой, а
– вектор, перпендикулярный прямой, а 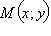 – произвольная точка этой прямой (см. рис. 11.5.3). Тогда M лежит на прямой тогда и только тогда, когда вектор
– произвольная точка этой прямой (см. рис. 11.5.3). Тогда M лежит на прямой тогда и только тогда, когда вектор 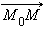 перпендикулярен вектору
перпендикулярен вектору 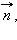 а для этого необходимо и достаточно, чтобы скалярное произведение векторов
а для этого необходимо и достаточно, чтобы скалярное произведение векторов 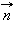 и
и 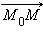 равнялось нулю:
равнялось нулю: 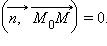 Введя радиус-векторы
Введя радиус-векторы 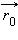 и
и 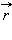 точек
точек 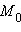 и M, это уравнение можно записать в виде
и M, это уравнение можно записать в виде 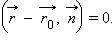 Это – нормальное векторное уравнение прямой, а
Это – нормальное векторное уравнение прямой, а 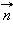 – нормальный вектор прямой. Если переписать его через координаты точек
– нормальный вектор прямой. Если переписать его через координаты точек 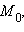 M и вектор
M и вектор 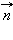 в ортогональной декартовой системе координат, получим
в ортогональной декартовой системе координат, получим
Это уравнение прямой, проходящей через данную точку 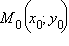 перпендикулярно вектору
перпендикулярно вектору 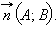 Обозначив
Обозначив 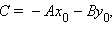 окончательно имеем
окончательно имеем
В § 11.4 было показано, что любая прямая может быть задана этим уравнением при условии 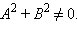 Назовем это уравнение общим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением Ax + By + C = 0, можно считать, что вектор
Назовем это уравнение общим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением Ax + By + C = 0, можно считать, что вектор 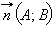 перпендикулярен прямой, а вектор
перпендикулярен прямой, а вектор 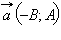 параллелен ей. Действительно, так как
параллелен ей. Действительно, так как 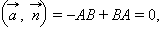 векторы
векторы 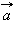 и
и 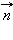 взаимно ортогональны, а поскольку
взаимно ортогональны, а поскольку 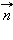 – нормальный вектор к прямой, то
– нормальный вектор к прямой, то 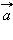 параллелен ей. Тогда
параллелен ей. Тогда 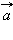 – направляющий вектор прямой.
– направляющий вектор прямой.
При рассмотрении векторно-параметрического уравнения прямой мы показали, как перейти к каноническому уравнению, из которого легко получить общее уравнение прямой. Аналогично, из нормального векторного уравнения так же легко перейти к общему уравнению прямой. Покажем теперь, как из общего уравнения прямой получить ее векторные уравнения.
Пусть прямая задана общим уравнением Ax + By + C = 0 в прямоугольной декартовой системе координат. Тогда мы знаем, что вектор 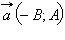 – направляющий вектор прямой,
– направляющий вектор прямой, 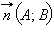 – ее нормальный вектор. Так как
– ее нормальный вектор. Так как 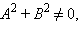 предположим для определенности, что A ≠ 0. Тогда точка
предположим для определенности, что A ≠ 0. Тогда точка 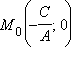 принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно,
принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно,
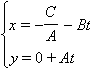 – векторно-параметрическое уравнение; – векторно-параметрическое уравнение;
|
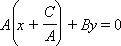 – векторное нормальное уравнение. – векторное нормальное уравнение.
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


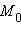 параллельно вектору
параллельно вектору 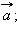
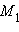 и
и 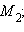
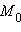 перпендикулярно вектору
перпендикулярно вектору 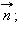
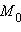 и составляет с вектором
и составляет с вектором 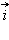 угол α (см. рис. 11.5.1).
угол α (см. рис. 11.5.1).

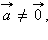 параллельный прямой
параллельный прямой 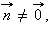 перпендикулярный прямой
перпендикулярный прямой 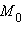 и
и 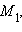 то вектор
то вектор 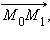 в частности, будет направляющим вектором прямой
в частности, будет направляющим вектором прямой 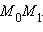
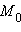 и направляющим вектором
и направляющим вектором 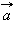 (см. рис. 11.5.2). Пусть
(см. рис. 11.5.2). Пусть 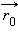 и
и 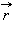 радиус-векторы точек
радиус-векторы точек 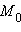 и
и 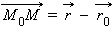 параллелен прямой, и, следовательно, вектору
параллелен прямой, и, следовательно, вектору 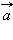 тогда и только тогда, когда
тогда и только тогда, когда 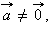 то
то
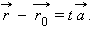
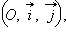 то уравнение можно записать в виде
то уравнение можно записать в виде
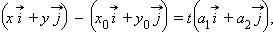
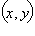 и
и 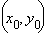 – координаты точек
– координаты точек 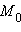 и
и 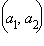 – координаты вектора
– координаты вектора 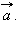 Отсюда следует, что
Отсюда следует, что
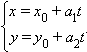
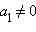 и
и 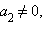 тогда из уравнений следует, что
тогда из уравнений следует, что 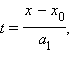
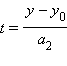 и, окончательно, уравнение
и, окончательно, уравнение 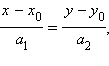 которое называется каноническим уравнением прямой, с направляющим вектором
которое называется каноническим уравнением прямой, с направляющим вектором 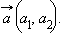
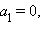 то параметрическое уравнение примет вид
то параметрическое уравнение примет вид
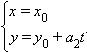
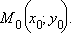 Каноническое уравнение прямой имеет вид
Каноническое уравнение прямой имеет вид 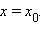 Аналогично, если
Аналогично, если 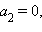 то прямая, задаваемая системой
то прямая, задаваемая системой
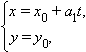
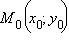 параллельно оси
параллельно оси 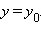
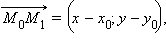 где
где 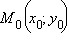 и
и 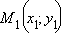 – произвольные две точки прямой. Тогда, подставив координаты вектора
– произвольные две точки прямой. Тогда, подставив координаты вектора 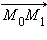 в каноническое уравнение, получим уравнение прямой, проходящей через две заданные точки:
в каноническое уравнение, получим уравнение прямой, проходящей через две заданные точки:
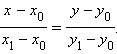
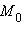 и
и 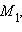 первая из которых лежит на оси
первая из которых лежит на оси 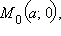 а вторая лежит на оси
а вторая лежит на оси 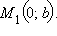 Подставляя их в уравнение, получим
Подставляя их в уравнение, получим
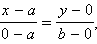
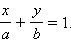
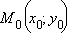 – некоторая точка прямой,
– некоторая точка прямой, 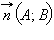 – вектор, перпендикулярный прямой, а
– вектор, перпендикулярный прямой, а 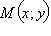 – произвольная точка этой прямой (см. рис. 11.5.3). Тогда
– произвольная точка этой прямой (см. рис. 11.5.3). Тогда 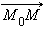 перпендикулярен вектору
перпендикулярен вектору 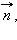 а для этого необходимо и достаточно, чтобы скалярное произведение векторов
а для этого необходимо и достаточно, чтобы скалярное произведение векторов 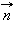 и
и 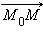 равнялось нулю:
равнялось нулю: 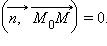 Введя радиус-векторы
Введя радиус-векторы 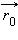 и
и 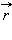 точек
точек 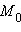 и
и 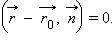 Это – нормальное векторное уравнение прямой, а
Это – нормальное векторное уравнение прямой, а 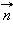 – нормальный вектор прямой. Если переписать его через координаты точек
– нормальный вектор прямой. Если переписать его через координаты точек 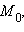
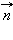 в ортогональной декартовой системе координат, получим
в ортогональной декартовой системе координат, получим
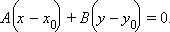
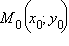 перпендикулярно вектору
перпендикулярно вектору 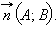 Обозначив
Обозначив 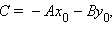 окончательно имеем
окончательно имеем
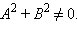 Назовем это уравнение общим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением
Назовем это уравнение общим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением 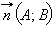 перпендикулярен прямой, а вектор
перпендикулярен прямой, а вектор 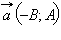 параллелен ей. Действительно, так как
параллелен ей. Действительно, так как 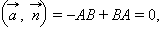 векторы
векторы 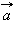 и
и 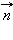 взаимно ортогональны, а поскольку
взаимно ортогональны, а поскольку 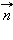 – нормальный вектор к прямой, то
– нормальный вектор к прямой, то 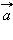 параллелен ей. Тогда
параллелен ей. Тогда 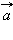 – направляющий вектор прямой.
– направляющий вектор прямой.
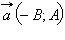 – направляющий вектор прямой,
– направляющий вектор прямой, 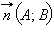 – ее нормальный вектор. Так как
– ее нормальный вектор. Так как 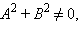 предположим для определенности, что
предположим для определенности, что 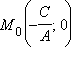 принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно,
принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно,
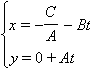 – векторно-параметрическое уравнение;
– векторно-параметрическое уравнение;
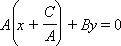 – векторное нормальное уравнение.
– векторное нормальное уравнение.




