 |
 |
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. Возьмем на координатной плоскости окружность радиуса
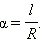 |
Такая мера называется радианной мерой угла и используется наравне с угловой. Говорят, что угол равен определённому числу радиан. Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу. В самом деле: 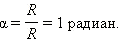 Обозначение радиана – «рад». Так как длина всей окружности радиуса
Обозначение радиана – «рад». Так как длина всей окружности радиуса 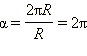 радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует
радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует 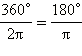 градусов:
градусов:
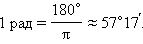 |
И наоборот,
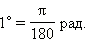 |
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
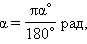 |
и от радианного измерения к градусному:
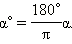 |
Обозначение «рад» при записи часто опускают и вместо, например,
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
|
||||||||||||||||||
| Таблица 2.4.1.1 |
Определите радианную меру угла, если его градусная мера равна: 1) 2°; 2) 225°.
Снова рассмотрим на координатной плоскости окружность радиуса
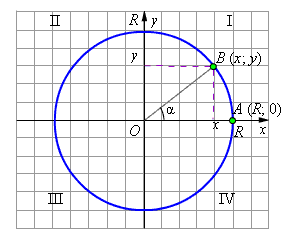 |
| Рисунок 2.4.1.1. Окружность радиуса |
Рассмотрим произвольный угол α. Изобразим его как угол поворота радиус-вектора 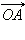 против часовой стрелки. При таком повороте точка
против часовой стрелки. При таком повороте точка 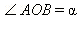 (α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка
(α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка
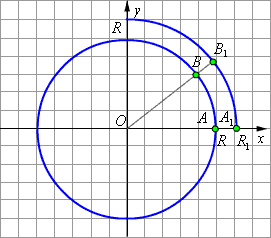 |
| Рисунок 2.4.1.2 |
Докажем, что отношения 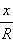 и
и 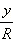 не зависят от величины радиуса
не зависят от величины радиуса 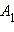 такую, что
такую, что 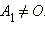 Построим окружность с центром в начале координат радиуса
Построим окружность с центром в начале координат радиуса 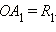 Построенная окружность пересекает радиус-вектор
Построенная окружность пересекает радиус-вектор 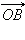 в точке
в точке 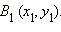 Так как векторы
Так как векторы 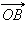 и
и 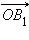 коллинеарны и одинаково направлены, то
коллинеарны и одинаково направлены, то
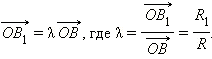 |
Однако равные векторы имеют равные координаты, следовательно,
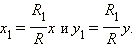 |
Откуда следует после деления обеих частей последних равенств на
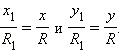 |
Итак, для любого угла поворота отношение координат радиус-вектора к его длине не зависит от этой длины радиус-вектора. Следовательно, отношения 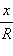 и
и 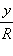 характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например,
характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например,

 |
|
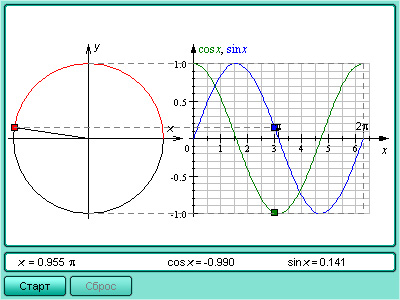
Модель 2.6.
Координатная окружность
|
Ввиду всего вышесказанного, рассмотренные отношения 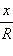 и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить. Введём несколько ключевых определений.
и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить. Введём несколько ключевых определений.
 |
 |
|
 |
 |
|

 |
|
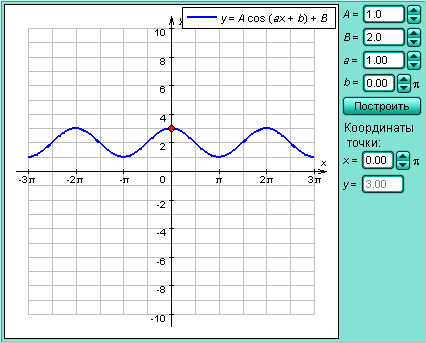
Модель 2.8.
Функция
|
 |
 |
|
 |
 |
|

 |
|
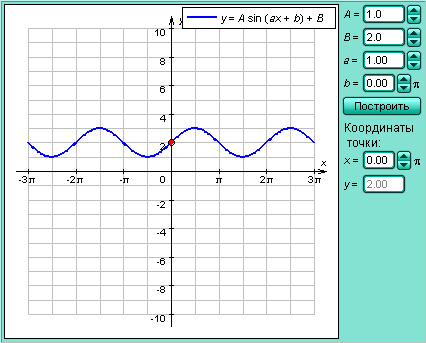
Модель 2.7.
Функция
|
 |
 |
|
 |
 |
|

 |
|
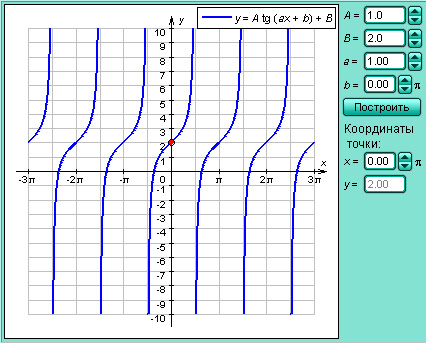
Модель 2.9.
Функция
|
 |
 |
|
 |
 |
|

 |
|
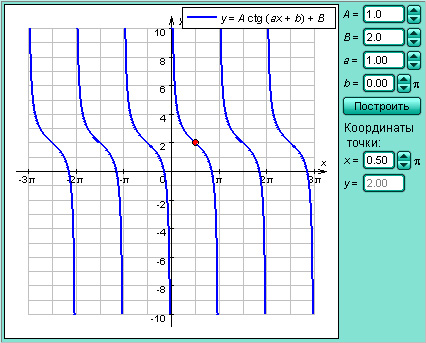
Модель 2.10.
Функция
|
Ясно, что для данного угла α функции 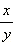 и
и 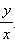 Значит,
Значит, 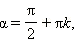 где
где 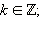
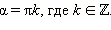
Поскольку синус по определению равен ординате точки на единичной окружности, а косинус − абсциссе, то знаки тригонометрических функций по четвертям будут такими:
|
|||||||||||||||||||||||||||||
| Таблица 2.4.1.2 | |||||||||||||||||||||||||||||
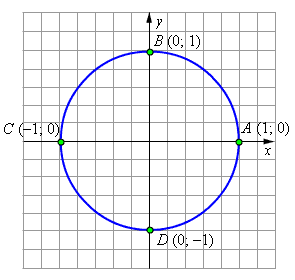 |
| Рисунок 2.4.1.3. Вычисление углов |
Найдём значения тригонометрических функций некоторых наиболее часто встречающихся углов. Конец радиус-вектора, отвечающего углу 0°, точка
Данные нами определения совпадают для острых углов с определениями тригонометрических функций в геометрии. В самом деле, например, синусом острого угла прямоугольного треугольника 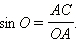 Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника.
Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника.
Однако если мы поместим наш прямоугольный треугольник так, что его вершина – точка
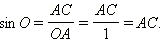 |
Значит, синус острого угла равен ординате точки, лежащей на тригонометрической окружности. А это как раз совпадает с нашим определением синуса. Совершенно те же самые рассуждения приводят нас к полной эквивалентности геометрического определения тригонометрических функций с тем, что дано в настоящем разделе. Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением.
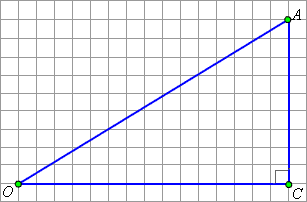 |
| Рисунок 2.4.1.4. Прямоугольный треугольник |
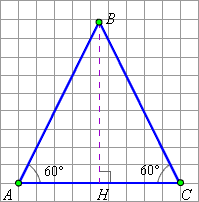 |
| Рисунок 2.4.1.5. Правильный треугольник |
Рассмотрим правильный треугольник
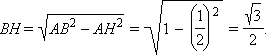 |
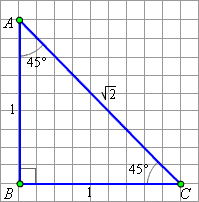 |
| Рисунок 2.4.1.6. Прямоугольный равнобедренный треугольник |
Значит, 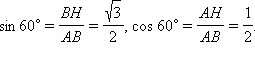 Рассматривая угол
Рассматривая угол 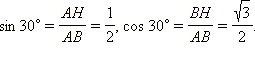 Соответственно,
Соответственно, 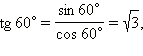
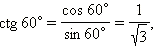
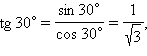
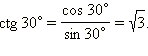
Рассмотрим теперь прямоугольный равнобедренный треугольник ![]() CAB = 45°
CAB = 45°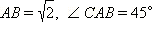 и
и 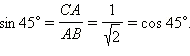 Следовательно,
Следовательно, 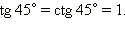
Итак, мы вычислили значения тригонометрических функций основных углов. Составим таблицу значений тригонометрических функций, которую мы только что получили.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица 2.4.1.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
|
 |
 |
|
Если функция 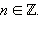 Поэтому говорят о наименьшем положительном периоде (НПП) функции
Поэтому говорят о наименьшем положительном периоде (НПП) функции
Аналогично можно показать, что функция
 |
 |
 |

