 |
 |
Пусть прямые 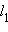 и
и 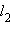 заданы общими уравнениями
заданы общими уравнениями
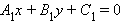 и и 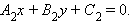 |
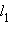 и
и 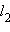 (напомним, что угол между прямыми измеряется от 0° до 90°), а через ψ – угол между нормальными векторами
(напомним, что угол между прямыми измеряется от 0° до 90°), а через ψ – угол между нормальными векторами 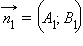 и
и 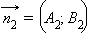 этих прямых. Если
этих прямых. Если 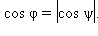 Из теоремы 11.10 следует, что
Из теоремы 11.10 следует, что
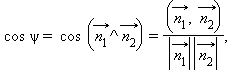 |
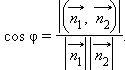 |
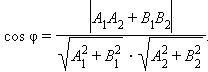 |
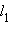 и
и 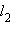 заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами 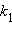 и
и 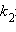
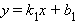 и и 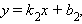 |
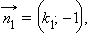
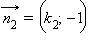 и выражение для косинуса угла между этими прямыми будет иметь вид:
и выражение для косинуса угла между этими прямыми будет иметь вид:
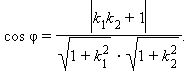 |
Из последнего выражения следует, что если 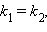 то
то
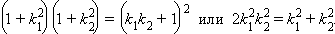 |
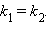
Если 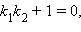 то
то 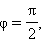 то есть прямые перпендикулярны. Обратно, если прямые перпендикулярны, то
то есть прямые перпендикулярны. Обратно, если прямые перпендикулярны, то 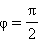 или
или 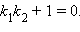
Следовательно, необходимые и достаточные условия параллельности и перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами 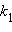 и
и 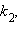 формулируются следующим образом.
формулируются следующим образом.

Для того чтобы прямые 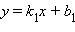 и
и 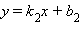 были
были
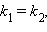
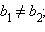
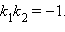
Пользуясь знанием координат направляющего и нормального векторов прямых, заданных общими уравнениями, можно сформулировать условия параллельности и перпендикулярности прямых через коэффициенты общих уравнений этих прямых.

Для того чтобы прямые 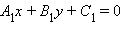 и
и 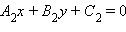 были
были
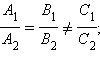
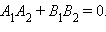
Пусть задана прямая 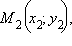 лежащая вне прямой. Поставим задачу найти расстояние
лежащая вне прямой. Поставим задачу найти расстояние 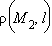 от этой точки до прямой
от этой точки до прямой 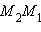 из точки
из точки 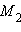 на прямую
на прямую 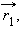
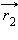 радиус-векторы точек
радиус-векторы точек 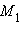 и
и 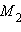 соответственно (см. рис. 11.6.1). Очевидно,
соответственно (см. рис. 11.6.1). Очевидно, 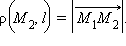
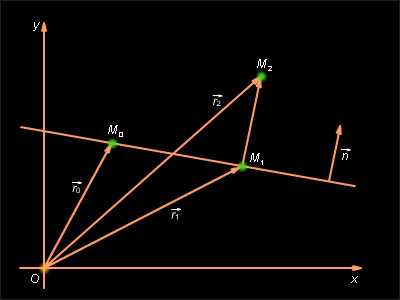
|
| Рисунок 11.6.1 |
Пусть 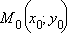 – некоторая точка прямой
– некоторая точка прямой 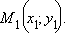 Тогда уравнение прямой
Тогда уравнение прямой
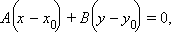 |
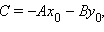 а
а 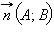 – вектор нормали к прямой
– вектор нормали к прямой 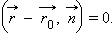
Очевидно, справедливо векторное равенство 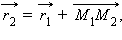 причем
причем 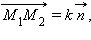 поэтому
поэтому 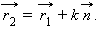 Умножив обе части равенства скалярно на вектор
Умножив обе части равенства скалярно на вектор 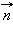 , получим
, получим
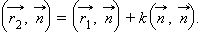 |
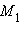 лежит на прямой
лежит на прямой 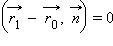 и, следовательно,
и, следовательно, 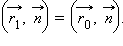 Подставляя в исходное равенство, найдем
Подставляя в исходное равенство, найдем
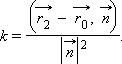 |
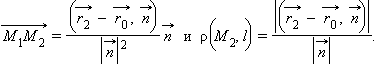 |
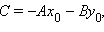
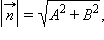 имеем
имеем
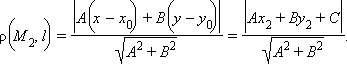 |
Таким образом верна теорема

Растояние 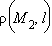 от точки
от точки 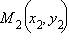 до прямой
до прямой
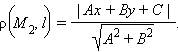 |
 |
 |
 |


| Фестул |
| Пилы Фестул: Официальный офис продаж! Кредит! Гарантия! Доставка! Жмите |
| ftrussia.ru |