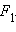Глава 10. Декартовы координаты
10.9. Гипербола и ее свойства
В § 7 было получено уравнение гиперболы. Перейдем к новой системе координат, как и в § 8.
В новой системе координат, которую называют также канонической, уравнение гиперболы имеет вид
Это уравнение называется каноническим уравнением гиперболы.
Отметим следующие свойства гиперболы.
Свойство 10.6.
Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называются вершинами гиперболы.
Для определения координат точек пересечения гиперболы с осью Oy нужно совместно решить их уравнения
Подставляя x = 0 в уравнение гиперболы, получим 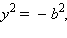 а это означает, что система не имеет решений. Следовательно, гипербола не пересекает ось ординат.
Для определения координат точек пересечения гиперболы с осью Ox нужно решить совместно их уравнения
Отсюда, подставляя y = 0 в уравнение гиперболы, получаем x = ±a.
Таким образом, точками пересечения гиперболы с осью Ox будут точки A (a; 0) и B (–a; 0).
|
Отрезок AB называется действительной осью гиперболы, его длина равна 2a. Число a называется действительной полуосью гиперболы, число b – мнимой полуосью.
Свойство 10.7.
Гипербола имеет две взаимно перпендикулярные оси симметрии.
Обоснование этого свойства аналогично тому, как обосновано свойство 10.3 для эллипса.
|
Свойство 10.8.
Гипербола имеет центр симметрии.
Если координаты точки M (x; y) удовлетворяют уравнению гиперболы, тому же уравнению удовлетворяют и координаты точки N (–x; –y). Точка N, очевидно, симметрична точке M относительно начала координат.
|
Центр симметрии гиперболы называют центром гиперболы.
Свойство 10.9.
Гипербола пересекается с прямой y = kx при 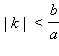 в двух точках. Если
в двух точках. Если 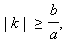 то общих точек у прямой и гиперболы нет.
то общих точек у прямой и гиперболы нет.
Для определения координат точек пересечения гиперболы и прямой y = kx нужно решить систему уравнений
Исключая y, получаем
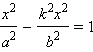 или или 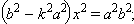 |
При 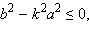 то есть при 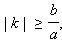 полученное уравнение, а потому и система решений не имеют. Прямые с уравнениями 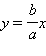 и 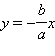 называются асимптотами гиперболы.
При 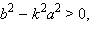 то есть при то есть при 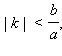 система имеет два решения: система имеет два решения:
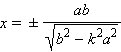 и и 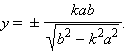 |
Следовательно, каждая прямая, проходящая через начало координат, с угловым коэффициентом, модуль которого меньше 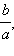 пересекает гиперболу в двух точках. При k = 0 получаем точки пересечения A (a; 0) и B (–a; 0) – вершины гиперболы.
|
Так как гипербола симметрична относительно осей координат, то достаточно изучить ее форму в первом квадранте координатной плоскости. Из полученных формул
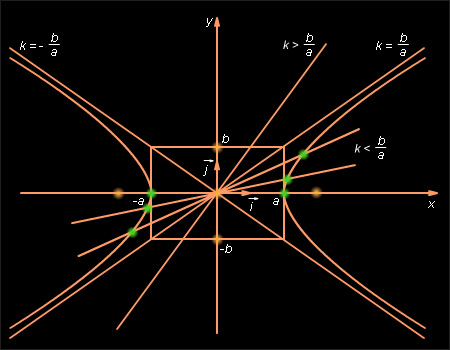
видно, что при возрастании k от нуля до 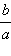 (при этом угол наклона прямой к оси Ox возрастает от нуля до некоторого значения) и абциссы, и ординаты точек пересечения прямой с гиперболой возрастают. Прямая y = kx пересекает гиперболу во все более далеких от начала координат точках. Таким образом, гипербола имеет вид, изображенный на рис. 10.9.1, и состоит из двух не связанных между собой частей, называемых ее ветвями.
(при этом угол наклона прямой к оси Ox возрастает от нуля до некоторого значения) и абциссы, и ординаты точек пересечения прямой с гиперболой возрастают. Прямая y = kx пересекает гиперболу во все более далеких от начала координат точках. Таким образом, гипербола имеет вид, изображенный на рис. 10.9.1, и состоит из двух не связанных между собой частей, называемых ее ветвями.
 1
|
| Рисунок 10.9.1
|
Точки 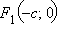 и
и 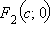 называются фокусами гиперболы. Здесь
называются фокусами гиперболы. Здесь 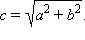
Величина 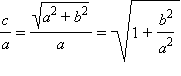 называется эксцентриситетом гиперболы и обозначается так же, как и в случае эллипса, буквой ε.
называется эксцентриситетом гиперболы и обозначается так же, как и в случае эллипса, буквой ε.
Из определения
Из формулы видно, что чем меньше эксцентриситет, тем более гипербола сжата к оси Ox.
В соответствии с обозначениями
Тогда, аналогично случаю с эллипсом,
Координаты точки A при переходе в новую систему координат будут равны
То есть точка A в новой системе координат имеет те же координаты, что и фокус 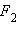 гиперболы, и поэтому совпадает с ним.
гиперболы, и поэтому совпадает с ним.
Уравнение же прямой l в новой системе координат будет иметь вид
Обозначим 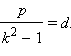 Так как
Так как 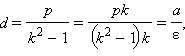 то, поскольку для гиперболы ε > 1, имеем d < a. Прямая x = d называется директрисой гиперболы, соответствующей фокусу
то, поскольку для гиперболы ε > 1, имеем d < a. Прямая x = d называется директрисой гиперболы, соответствующей фокусу 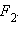 Прямую x = –d называют директрисой, соответствующей фокусу
Прямую x = –d называют директрисой, соответствующей фокусу 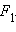
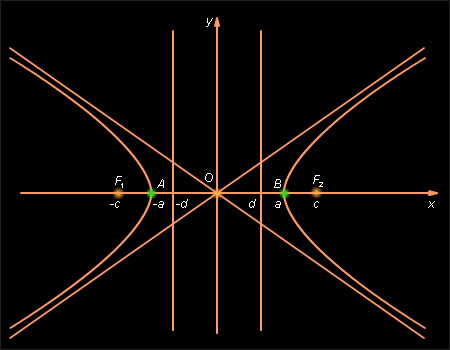
С учетом симметрии гиперболы относительно осей координат, свойство, с помощью которого определили гиперболу, в новых терминах можно сформулировать так же, как и в случае эллипса: отношение расстояния от любой точки гиперболы до одного из его фокусов к расстоянию от этой точки до соответствующей ему директрисы есть величина постоянная и равная эксцентриситету. Вид гиперболы и ее директрис в канонической системе координат приведен на рис. 10.9.2.
 2
|
| Рисунок 10.9.2
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


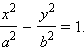
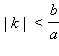 в двух точках. Если
в двух точках. Если 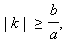 то общих точек у прямой и гиперболы нет.
то общих точек у прямой и гиперболы нет.
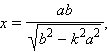
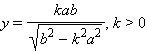
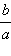 (при этом угол наклона прямой к оси
(при этом угол наклона прямой к оси 
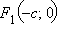 и
и 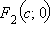 называются фокусами гиперболы. Здесь
называются фокусами гиперболы. Здесь 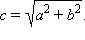
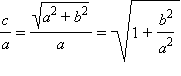 называется эксцентриситетом гиперболы и обозначается так же, как и в случае эллипса, буквой ε.
называется эксцентриситетом гиперболы и обозначается так же, как и в случае эллипса, буквой ε.
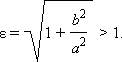
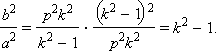
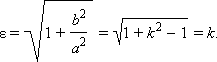
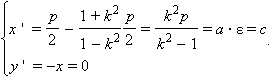
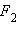 гиперболы, и поэтому совпадает с ним.
гиперболы, и поэтому совпадает с ним.
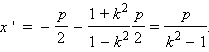
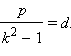 Так как
Так как 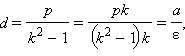 то, поскольку для гиперболы
то, поскольку для гиперболы 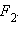 Прямую
Прямую