
Учебник. Исходные понятия и определения
Пусть задана совокупность из n точек. Перенумеруем их каким-либо образом с помощью первых n натуральных чисел и запишем в порядке возрастания номеров (A1, A2, ... , An). Такую совокупность будем называть упорядоченной. Точки, номера которых отличаются на единицу, назовем соседними. Ломаной A1A2... An называется фигура, которая состоит из упорядоченной совокупности точек и отрезков, соединяющих соседние среди них. Точки A1, A2, ... , An называются вершинами, а отрезки A1A2, A2A3, ... , An – 1An – звеньями ломаной. Звенья, имеющие общий конец, назовем смежными, а точки A1 и An – концами ломаной. Ломаная называется простой, если несмежные ее звенья не имеют общих точек. Ломаная называется замкнутой, если ее концы соединены отрезком. Этот отрезок также называется звеном, а концы ломаной считаются соседними вершинами.
На рис. 9.1.1 а показана простая ломаная, а на рис. 9.1.1 б, в, г – ломаные с самопересечением.
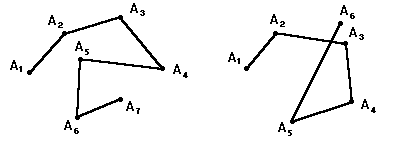
Простая замкнутая ломаная называется многоугольником, если ее смежные звенья не лежат на одной прямой. Вершины ломаной называются вершинами многоугольника, а звенья ломаной – сторонами. Диагоналями многоугольника называются отрезки, соединяющие несоседние вершины многоугольника.
Плоским многоугольником называется конечная часть плоскости, ограниченная многоугольником – его границей. Точки плоского многоугольника, отличные от точек его границы, называются внутренними. Многоугольной фигурой называется объединение конечного числа плоских многоугольников. Многоугольные фигуры не перекрываются, если они не имеют общих внутренних точек. Многоугольная фигура называется составленной из данных многоугольных фигур (разбитой на данные многоугольные фигуры), если она является их объединением, а сами эти фигуры не перекрываются.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".