
Учебник. Проведение прямой, параллельной данной
Через заданную точку A провести прямую, параллельную данной прямой a.
Анализ. Если A ∈ a, то задача не имеет решения, поэтому, пусть A лежит вне прямой a, и b || a – искомая прямая. Через точку A проведем секущую (AB), B ∈ a. По свойству параллельных прямых внутренние накрест лежащие углы при параллельных прямых и секущей равны. Верно и обратное: если внутренние накрест лежащие углы при прямых a и b и секущей AB равны, то a || b. Отсюда способ построения.
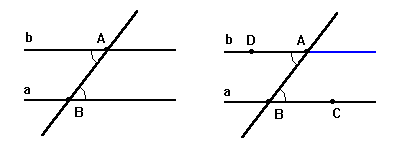
Построение. Через заданную точку A и произвольную точку B прямой a проведем прямую AB. Пусть C – произвольная, отличная от B точка прямой a. Построим от луча AB в полуплоскость, не содержащую точку C, угол, равный углу (ABC). Пусть [AD) – сторона построенного угла. Тогда прямая AD || a.
Через точку A проведите прямую, параллельную данной.
Доказательство следует из признака параллельности прямых (теорема 3.1), ввиду равенства углов (ABC) и (BAD) как внутренних накрест лежащих при прямых a, (AD) и секущей (AB).
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".