
Учебник. Вычисление значений синуса, косинуса и тангенса некоторых углов
Вычисление значений синуса, косинуса и тангенса некоторых углов
Рассмотрим прямоугольный равнобедренный треугольник с углом при основании, равным 45°. Пусть катеты его равны a. Тогда по теореме Пифагора его гипотенуза будет равна Поэтому
Рассмотрим равносторонний треугольник ABC со стороной, равной a. Проведем в нем медиану BD. Получим треугольник ABD – прямоугольный с острым углом при вершине B и стороной По теореме Пифагора Значит:
Составим таблицу известных углов и значений синуса, косинуса и тангенса для них.
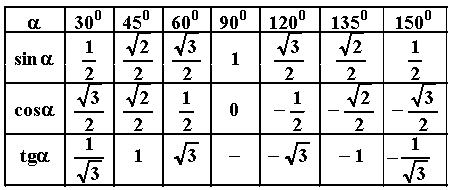
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".