Открытая Математика. Планиметия. Вычисление угла между прямыми

Вычисление угла между прямыми

Пусть прямые $l_{1}$ и $l_{2}$ заданы общими уравнениями $A_{1} x + B_{1} y + C_{1} = 0$ и $A_{2} x + B_{2} y + C_{2} = 0 .$ Обозначим через φ величину угла между прямыми $l_{1}$ и $l_{2}$ (напомним, что угол между прямыми измеряется от 0° до 90°), а через ψ – угол между нормальными векторами $\overset{⟶}{n_{1}} = (A_{1}; B_{1})$ и $\overset{⟶}{n_{2}} = (A_{2}; B_{2})$ этих прямых. Если ψ ≤ 90°, то φ = ψ. Если же ψ > 90°, то φ = 180° – ψ. В обоих случаях верно равенство $cos φ = | cos ψ | .$ Из теоремы 11.10 следует, что $cos ψ = cos (\overset{⟶}{n_{1}}^\overset{⟶}{n_{2}}) = \frac{(\overset{⟶}{n_{1}}, \overset{⟶}{n_{2}})}{| \overset{⟶}{n_{1}} | | \overset{⟶}{n_{2}} |},$ и, следовательно, $cos φ = \frac{| (\overset{⟶}{n_{1}}, \overset{⟶}{n_{2}}) |}{| \overset{⟶}{n_{1}} | | \overset{⟶}{n_{2}} |} .$ Записав через координаты, получим $cos φ = \frac{| A_{1} A_{2} + B_{1} B_{2} |}{\sqrt{A_{1}^{2} + B_{1}^{2}} ċ \sqrt{A_{2}^{2} + B_{2}^{2}}} .$ Если прямые $l_{1}$ и $l_{2}$ заданы уравнениями с угловыми коэффициентами $k_{1}$ и $k_{2} :$ $y = k_{1} x + b_{1}$ и $y = k_{2} x + b_{2},$ то нормальные векторы этих прямых могут быть $\overset{⟶}{n_{1}} = (k_{1}; - 1),$ $\overset{⟶}{n_{2}} = (k_{2}; - 1)$ и выражение для косинуса угла между этими прямыми будет иметь вид: $cos φ = \frac{| k_{1} k_{2} + 1 |}{\sqrt{1 + k_{1}^{2}} ċ \sqrt{1 + k_{2}^{2}}} .$

Из последнего выражения следует, что если $k_{1} = k_{2},$ то cos φ = 1 и φ = 0, то есть прямые параллельны или совпадают. С другой стороны, если прямые параллельны, то φ = 0 или cos φ = 1. Подставляя в правую часть вместо cos φ его значение 1, умножая обе части на знаменатель и возводя в квадрат, получим $(1 + k_{1}^{2}) (1 + k_{2}^{2}) = {(k_{1} k_{2} + 1)}^{2} или 2 k_{1}^{2} k_{2}^{2} = k_{1}^{2} + k_{2}^{2} .$ Отсюда получаем $k_{1} = k_{2} .$

Если $k_{1} k_{2} + 1 = 0,$ то cos φ = 0 и $φ = \frac{π}{2},$ то есть прямые перпендикулярны. Обратно, если прямые перпендикулярны, то $φ = \frac{π}{2}$ или cos φ = 0. Отсюда следует с необходимостью $k_{1} k_{2} + 1 = 0 .$

Следовательно, необходимые и достаточные условия параллельности и перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами $k_{1}$ и $k_{2},$ формулируются следующим образом.

Для того чтобы прямые $y = k_{1} x + b_{1}$ и $y = k_{2} x + b_{2}$ были

параллельны, необходимо и достаточно, чтобы $k_{1} = k_{2},$ $b_{1} \neq b_{2};$
перпендикулярны, необходимо и достаточно, чтобы $k_{1} k_{2} = - 1 .$

Пользуясь знанием координат направляющего и нормального векторов прямых, заданных общими уравнениями, можно сформулировать условия параллельности и перпендикулярности прямых через коэффициенты общих уравнений этих прямых.

Для того чтобы прямые $A_{1} x + B_{1} y + C_{1} = 0$ и $A_{2} x + B_{2} y + C_{2} = 0$ были

параллельны, необходимо и достаточно, чтобы соответствующие коэффициенты их уравнений при одноименных неизвестных были пропорциональны, то есть $\frac{A_{1}}{A_{2}} = \frac{B_{1}}{B_{2}} \neq \frac{C_{1}}{C_{2}};$
перпендикулярны, необходимо и достаточно, чтобы выполнялось равенство $A_{1} A_{2} + B_{1} B_{2} = 0 .$

Пусть $\overset{⟶}{a_{1}} (- B_{1}; A_{1}),$ $\overset{⟶}{a_{2}} = (- B_{2}; A_{2})$ – направляющие векторы прямых. Тогда необходимым и достаточным условием параллельности прямых является условие коллинеарности векторов $\overset{⟶}{a_{1}}$ и $\overset{⟶}{a_{2}},$ то есть $\overset{⟶}{a_{1}} = k \overset{⟶}{a_{2}} или {\begin{array}{l} - B_{1} = k (- B_{2}) \\ A_{1} = k A_{2} \end{array} .$ Так как при этом $\overset{⟶}{a_{1}} \neq \overset{⟶}{0}$ и $\overset{⟶}{a_{2}} \neq \overset{⟶}{0},$ то k ≠ 0. Поэтому, если один из коэффициентов равен нулю, например $A_{1} = 0,$ то с необходимостью $A_{1} = 0 .$ При этом $B_{1} \neq 0,$ $B_{2} \neq 0 .$ С учетом этого можно записать $\frac{A_{1}}{A_{2}} = \frac{B_{1}}{B_{2}},$ откуда формально следует $\frac{A_{1}}{A_{2}} = \frac{B_{1}}{B_{2}} = k .$ Отметим при этом, что если одновременно $\frac{C_{1}}{C_{2}} = k,$ то оба уравнения задают одну и ту же прямую и в этом случае прямые совпадают. Если же $\frac{A_{1}}{A_{2}} = \frac{B_{1}}{B_{2}} \neq \frac{C_{1}}{C_{2}},$ то прямые параллельны.
Неоходимым и достаточным условием перпендикулярности прямых является условие ортогональности их направляющих векторов $\overset{⟶}{a_{1}} (- B_{1}; A_{1})$ и $\overset{⟶}{a_{2}} (- B_{2}; A_{2}),$ для чего, в свою очередь, необходимо и достаточно равенство нулю их скалярного произведения, то есть $(\overset{⟶}{a_{1}}, \overset{⟶}{a_{2}}) = 0, или A_{1} A_{2} + B_{1} B_{2} = 0,$ что и требовалось доказать.

Пусть задана прямая l общим уравнением Ax + By + C = 0 и некоторая точка $M_{2} (x_{2}; y_{2}),$ лежащая вне прямой. Поставим задачу найти расстояние $ρ (M_{2}, l)$ от этой точки до прямой l. Опустим перпендикуляр $M_{2} M_{1}$ из точки $M_{2}$ на прямую l и обозначим $\overset{⟶}{r_{1}},$ $\overset{⟶}{r_{2}}$ радиус-векторы точек $M_{1}$ и $M_{2}$ соответственно (см. рис. 11.6.1). Очевидно, $ρ (M_{2}, l) = | \overset{⟶}{M_{1} M_{2}} | .$

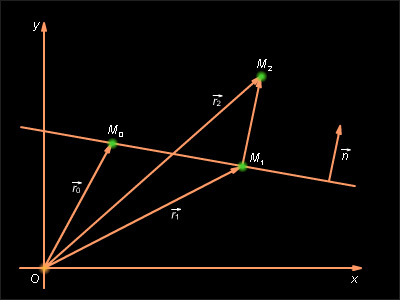
Пусть $M_{0} (x_{0}; y_{0})$ – некоторая точка прямой l, отличная от точки $M_{1} (x_{1}; y_{1}) .$ Тогда уравнение прямой l можно записать в нормальной векторной форме: $A (x - x_{0}) + B (y - y_{0}) = 0,$ где $C = - A x_{0} - B y_{0},$ а $\overset{⟶}{n} (A; B)$ – вектор нормали к прямой l. Или, в векторной форме, $(\overset{⟶}{r} - \overset{⟶}{r_{0}}, \overset{⟶}{n}) = 0 .$

Очевидно, справедливо векторное равенство $\overset{⟶}{r_{2}} = \overset{⟶}{r_{1}} + \overset{⟶}{M_{1} M_{2}},$ причем $\overset{⟶}{M_{1} M_{2}} = k \overset{⟶}{n},$ поэтому $\overset{⟶}{r_{2}} = \overset{⟶}{r_{1}} + k \overset{⟶}{n} .$ Умножив обе части равенства скалярно на вектор $\overset{⟶}{n}$ , получим $(\overset{⟶}{r_{2}}, \overset{⟶}{n}) = (\overset{⟶}{r_{1}}, \overset{⟶}{n}) + k (\overset{⟶}{n}, \overset{⟶}{n}) .$ Так как точка $M_{1}$ лежит на прямой l, то $(\overset{⟶}{r_{1}} - \overset{⟶}{r_{0}}, \overset{⟶}{n}) = 0$ и, следовательно, $(\overset{⟶}{r_{1}}, \overset{⟶}{n}) = (\overset{⟶}{r_{0}}, \overset{⟶}{n}) .$ Подставляя в исходное равенство, найдем $k = \frac{(\overset{⟶}{r_{2}} - \overset{⟶}{r_{0}}, \overset{⟶}{n})}{{| \overset{⟶}{n} |}^{2}} .$ Отсюда $\overset{⟶}{M_{1} M_{2}} = \frac{(\overset{⟶}{r_{2}} - \overset{⟶}{r_{0}}, \overset{⟶}{n})}{{| \overset{⟶}{n} |}^{2}} \overset{⟶}{n} и ρ (M_{2}, l) = \frac{| (\overset{⟶}{r_{2}} - \overset{⟶}{r_{0}}, \overset{⟶}{n}) |}{| \overset{⟶}{n} |} .$ Переходя к координатной форме записи и учитывая, что $C = - A x_{0} - B y_{0},$ $| \overset{⟶}{n} | = \sqrt{A^{2} + B^{2}},$ имеем $ρ (M_{2}, l) = \frac{| A (x - x_{0}) + B (y - y_{0}) |}{\sqrt{A^{2} + B^{2}}} = \frac{| A x_{2} + B y_{2} + C |}{\sqrt{A^{2} + B^{2}}} .$

Таким образом верна теорема

Растояние $ρ (M_{2}, l)$ от точки $M_{2} (x_{2}, y_{2})$ до прямой l, заданной уравнением Ax + By + C = 0 вычисляется по формуле $ρ (M_{2}, l) = \frac{| A x + B y + C |}{\sqrt{A^{2} + B^{2}}} .$

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Вычисление угла между прямыми

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ