
Учебник. Окружность Аполлония
Рассмотрим задачу: найти геометрическое место точек плоскости, отношение расстояний от которых до двух данных точек – величина постоянная. Для решения этой задачи используем метод координат, а именно: получим уравнение фигуры, образуемой ГМТ, а далее изучим ее геометрические свойства.
Введем прямоугольную систему координат, выбрав в качестве ее начала одну из двух заданных точек A и B (например, B), а ось Оx – так, чтобы вторая точка (пусть это будет точка A) лежала на положительной полуоси (см. рис. 10.6.1).
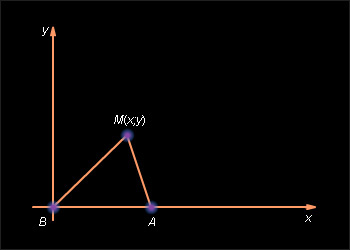
В данной системе координат точка B имеет координаты (0; 0), а точка A – (a; 0), где a > 0. Пусть M (x, y) – произвольная точка, удовлетворяющая условию задачи, то есть AM = k ċ BM, где k – заданное положительное число. Если k = 1, то это означает, что искомое множество состоит из точек, равноудаленных от данных точек A и B. Из свойств серединного перпендикуляра к отрезку следует, что искомым множеством в этом случае будет прямая, проходящая через середину отрезка AB перпендикулярно оси OX. Пусть теперь k ≠ 1. Из теоремы 10.2 имеем и условие принадлежности точки M искомому множеству можно записать в виде
Это равенство эквивалентно равенствам
Выделяя полный квадрат, получим
Это уравнение окружности с центром в точке лежащей на оси OX, и радиуса
Полученная окружность носит имя древнегреческого геометра Аполлония, решившего поставленную задачу чисто геометрическим методом.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".