Учебник. Парабола и ее свойства

В § 7 мы получили уравнение фигуры, каждая точка которой равноудалена от данной точки A и данной прямой l, и назвали ее параболой. В выбранной системе координат ее уравнение имело вид $y=\frac{1}{2p}{x}^2\mathrm{.}$ Сделаем поворот системы координат на угол 90°, воспользовавшись формулами поворота $\{\begin{array}{l}x=\mathrm{x\text{'}}cos90{}^{ˆ}-\mathrm{y\text{'}}sin90{}^{ˆ}=\mathrm{-}\mathrm{y\text{'}}\hfill \\ y=\mathrm{x\text{'}}sin90{}^{ˆ}+\mathrm{y\text{'}}cos90{}^{ˆ}=\mathrm{x\text{'}}\hfill \end{array}\mathrm{.}$ Запишем уравнение параболы в новой, канонической системе координат: ${\mathrm{y\text{'}}}^2=2p\mathrm{x\text{'}}\mathrm{.}$ Это уравнение называется каноническим уравнением параболы. В дальнейшем знак «штрих» при переменных для удобства мы будем опускать.

Приведем следующие свойства параболы:

Ось симметрии называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. Вершина параболы в канонической системе координат находится в начале координат.

При замене системы координат заданная в условии точка A с координатами $\left(0\mathrm{; }\frac{p}{2}\right)$  будет иметь новые координаты, определяемые из соотношений $\{\begin{array}{l}\mathrm{y\text{'}}=\mathrm{-}\mathrm{x\text{'}}=0\mathrm{,}\hfill \\ \mathrm{x\text{'}}=y=\frac{p}{2}\mathrm{.}\hfill \end{array}$ Таким образом, точка A будет иметь в канонической системе координаты $\left(\frac{p}{2}\mathrm{; }0\right)\mathrm{.}$  Данную точку $\left(\frac{p}{2}\mathrm{; }0\right)$  называют фокусом параболы и обозначают буквой F.

Прямая l, задаваемая в старой системе координат уравнением $y=\mathrm{-}\frac{p}{2}\mathrm{,}$  в новой системе координат будет иметь вид $\mathrm{x\text{'}}=\mathrm{-}\frac{p}{2}\mathrm{,}$  или, опуская штриховку, $x=\mathrm{-}\frac{p}{2}\mathrm{.}$

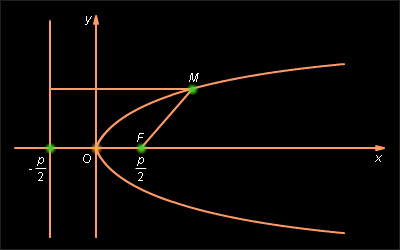
Данная прямая в канонической системе координат называется директрисой параболы. Расстояние от нее до фокуса называется фокальным параметром параболы. Очевидно, он равен p. Эксцентриситет параболы по определению полагают равным единице, то есть ε = k = 1.

Теперь свойство, через которое мы определили параболу, в новых терминах можно сформулировать следующим образом: любая точка параболы равноудалена от ее фокуса и директрисы.

Вид параболы в канонической системе координат и расположение ее директрисы приведены на рис. 10.10.1.