Заметим, что проекции фигуры на произвольные из параллельных плоскостей равны, так как могут быть совмещены параллельным переносом в направлении проектирования.

Теперь рассмотрим теорему для случая, когда проектируется треугольник.

Первый случай. Плоскость проекции проходит через сторону треугольника (чертеж 3.7.1), Пр_α(Δ ABC) = Δ ABO, CD – высота Δ ABC. По теореме о трех перпендикулярах OD 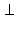 AB, то есть OD – высота Δ ABO. Плоскость CDO перпендикулярна прямой AB, поэтому 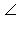CDO – линейный угол двугранного угла AB. Пусть 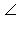CDO = φ, тогда OD = CD cos φ,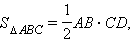

что и требовалось доказать.

Если сторона AB не лежит в плоскости проекции, но параллельна ей, доказательство аналогично.

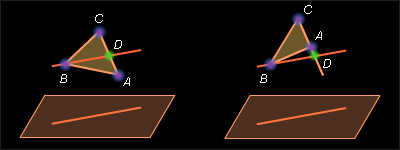
Второй случай. Ни одна сторона Δ ABC не параллельна плоскости проекции (чертеж 3.7.2). Проведем отрезок BD параллельно плоскости проекции. Тогда в каждом из треугольников ABD и BCD существует сторона BD, параллельная плоскости проекции. В соответствии с первым случаем получаем:

SΔ AB1D1 = SΔ ABD cos φ,  SΔ B1C1D1 = SΔ BCD cos φ.

Складывая или вычитая эти равенства в зависимости от того принадлежит точка D отрезку AC или лежит вне него, имеем

SΔ AB1C1 = SΔ ABC cos φ,

что и требовалось доказать.

Третий случай. Плоскость Δ перпендикулярна плоскости проекции. Проекцией Δ в этом случае является отрезок, площадь которого равна нулю. Косинус угла между плоскостью проекции и плоскостью Δ равен так же нулю. Значит формула 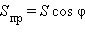также формально верна.

Если проектируется многоугольник, то разбиваем его на треугольники и для каждого применяем доказанную теорему.

1

Рисунок 3.7.1