Глава 2. Параллельность в пространстве
2.1. Параллельность прямых
Определение 2.1.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
Если две прямые a и b параллельны, то, как и в планиметрии, пишут a || b. В пространстве прямые могут быть размещены так, что они не пересекаются и не параллельны. Этот случай является особым для стереометрии.
Определение 2.2.
Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.
Теорема 2.1.
Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.
Пусть A 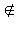 a (чертеж 2.1.1). Прямая a и точка A определяют единственную плоскость α. В этой плоскости проведем через точку A прямую b, параллельную прямой a. Если существует еще одна прямая c, параллельная a и проходящая через точку A, то по определению параллельных прямых c и a определяют некоторую плоскость. Эта плоскость содержит прямую a и точку A, то есть совпадает с плоскостью α. Следовательно, в плоскости α через точку A проходят две прямые, параллельные прямой a, что противоречит аксиоме о параллельных прямых в планиметрии. a (чертеж 2.1.1). Прямая a и точка A определяют единственную плоскость α. В этой плоскости проведем через точку A прямую b, параллельную прямой a. Если существует еще одна прямая c, параллельная a и проходящая через точку A, то по определению параллельных прямых c и a определяют некоторую плоскость. Эта плоскость содержит прямую a и точку A, то есть совпадает с плоскостью α. Следовательно, в плоскости α через точку A проходят две прямые, параллельные прямой a, что противоречит аксиоме о параллельных прямых в планиметрии.
|
Замечание. Согласно определению, две параллельные прямые лежат в одной плоскости. Легко заметить, что через две параллельные прямые можно провести только одну плоскость.
Теорема 2.2. Признак скрещивающихся прямых.
Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти две прямые скрещиваются.
Лемма 2.1.
Если одна из двух параллельных прямых пересекает плоскость, то и другая пересекает эту плоскость.
Пусть a || b и a 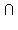 α = A (чертеж 2.1.3). Параллельные прямые a и b определяют некоторую плоскость β. Плоскости α и β имеют общую точку A, а, следовательно, имеют и общую прямую c, проходящую через точку A по аксиоме 1.2. Через точку A можно провести только одну прямую a, параллельную b. Следовательно, c не параллельна b. Прямые b и c не параллельны и лежат в одной плоскости β, следовательно, пересекаются в некоторой точке B. Прямая b имеет с плоскостью α общую точку B и не лежит в плоскости α (иначе по теореме 2.2 a и b были бы скрещивающимися). Следовательно, прямая b пересекает плоскость α. Лемма доказана. α = A (чертеж 2.1.3). Параллельные прямые a и b определяют некоторую плоскость β. Плоскости α и β имеют общую точку A, а, следовательно, имеют и общую прямую c, проходящую через точку A по аксиоме 1.2. Через точку A можно провести только одну прямую a, параллельную b. Следовательно, c не параллельна b. Прямые b и c не параллельны и лежат в одной плоскости β, следовательно, пересекаются в некоторой точке B. Прямая b имеет с плоскостью α общую точку B и не лежит в плоскости α (иначе по теореме 2.2 a и b были бы скрещивающимися). Следовательно, прямая b пересекает плоскость α. Лемма доказана.
|
Теорема 2.3. Транзитивность параллельности.
Две прямые, параллельные третьей, параллельны между собой. Другими словами, если a || c и b || c, то a || b.
Пусть a || c и b || c (чертеж 2.1.4). Заметим, что прямые a и b по теореме 2.1 не могут пересекаться, то есть если бы у них была одна точка, то через эту точку можно было бы провести единственную прямую, параллельную прямой c, то есть они бы совпадали. Докажем, что прямые a и b лежат в одной плоскости. Пусть A 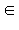 a. Проведем плоскость γ через прямую b и точку A и докажем, что a a. Проведем плоскость γ через прямую b и точку A и докажем, что a 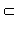 γ. Если a пересекает плоскость γ, то по лемме 2.1 c пересекает плоскость γ, и b пересекает плоскость γ. Мы пришли к противоречию, так как b γ. Если a пересекает плоскость γ, то по лемме 2.1 c пересекает плоскость γ, и b пересекает плоскость γ. Мы пришли к противоречию, так как b 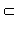 γ. Итак, a γ. Итак, a 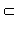 γ, b γ, b 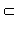 γ и a и b не имеют общих точек, следовательно a || b. γ и a и b не имеют общих точек, следовательно a || b.
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".












