 |
 |
Три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины треугольника.
Длина медианы треугольника выражается формулой 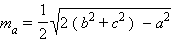 , где
, где
Длина стороны треугольника выражается формулой 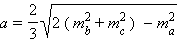 , где
, где
Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим сторонам.
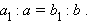 |
Длина биссектрисы треугольника выражается формулой 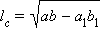 , где
, где
Длина биссектрисы треугольника выражается через длины его сторон
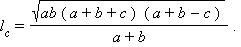 |
Для любого треугольника зависимость между его высотами 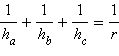 .
.
Высота равнобокой трапеции, в которую можно вписать окружность, является средним геометрическим его оснований 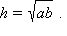
 |
 |
 |

