Глава 8. Построение фигур
8.5. Построение угла, равного данному
Отложить от данного луча в данную полуплоскость угол, равный данному углу.
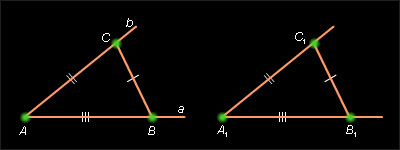
Анализ. Пусть a – данный луч с вершиной A, а угол (ab) искомый. Выберем точки B и C на лучах a и b соответственно. Соединив точки B и C, получим треугольник ABC. В равных треугольниках соответственные углы равны, и отсюда вытекает способ построения. Если на сторонах данного угла каким-то удобным образом выбрать точки C и B, от данного луча в данную полуплоскость построить треугольник AB1C1, равный ABC (а это можно сделать, если знать все стороны треугольника, см. предыдущую задачу), то задача будет решена.
 1
|
| Рисунок 8.5.1. Построение угла, равного данному. Анализ
|
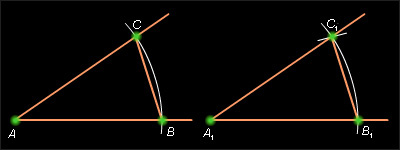
Построение. Проведем окружность с центром в вершине данного угла. Пусть B и C – точки пересечения окружности со сторонами угла. Радиусом AB проведем окружность с центром в точке A1 – начальной точке данного луча. Точку пересечения этой окружности с данным лучом обозначим B1. Опишем окружность с центром в B1 и радиусом BC. Точка пересечения C1 построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.
 2
|
| Рисунок 8.5.2. Построение угла, равного данному. Построение
|
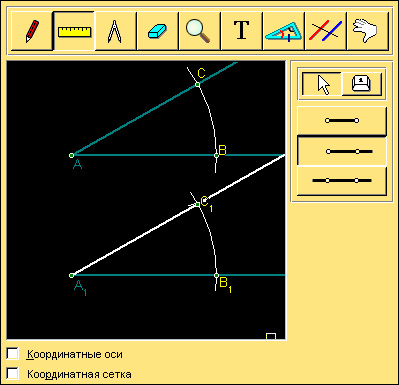
Требуется построить угол, равный данному. Угол следует откладывать в верхнюю полуплоскость относительно данного луча.

 |
|
Модель 8.5.
Построение угла равного данному
|
Треугольники ABC и A1B1C1 равны по трем сторонам. Углы A и A1 – соответствующие углы этих треугольников. Следовательно, 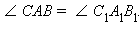
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".










