

 Задачи с решениями
Задачи с решениями

Доказать, что высота равнобокой трапеции, в которую можно вписать окружность, является средним геометрическим ее оснований.
Решение
Так как в четырехугольнике, описанном около окружности, суммы длин противоположных сторон равны, то
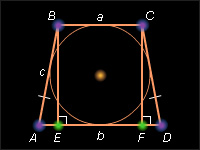 |
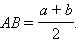 Далее имеем, что проекция боковой стороны на основание
Далее имеем, что проекция боковой стороны на основание  Действительно, прямоугольные треугольники
Действительно, прямоугольные треугольники 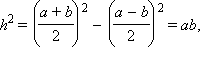 или
или
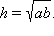
 3 из 6
3 из 6
 |